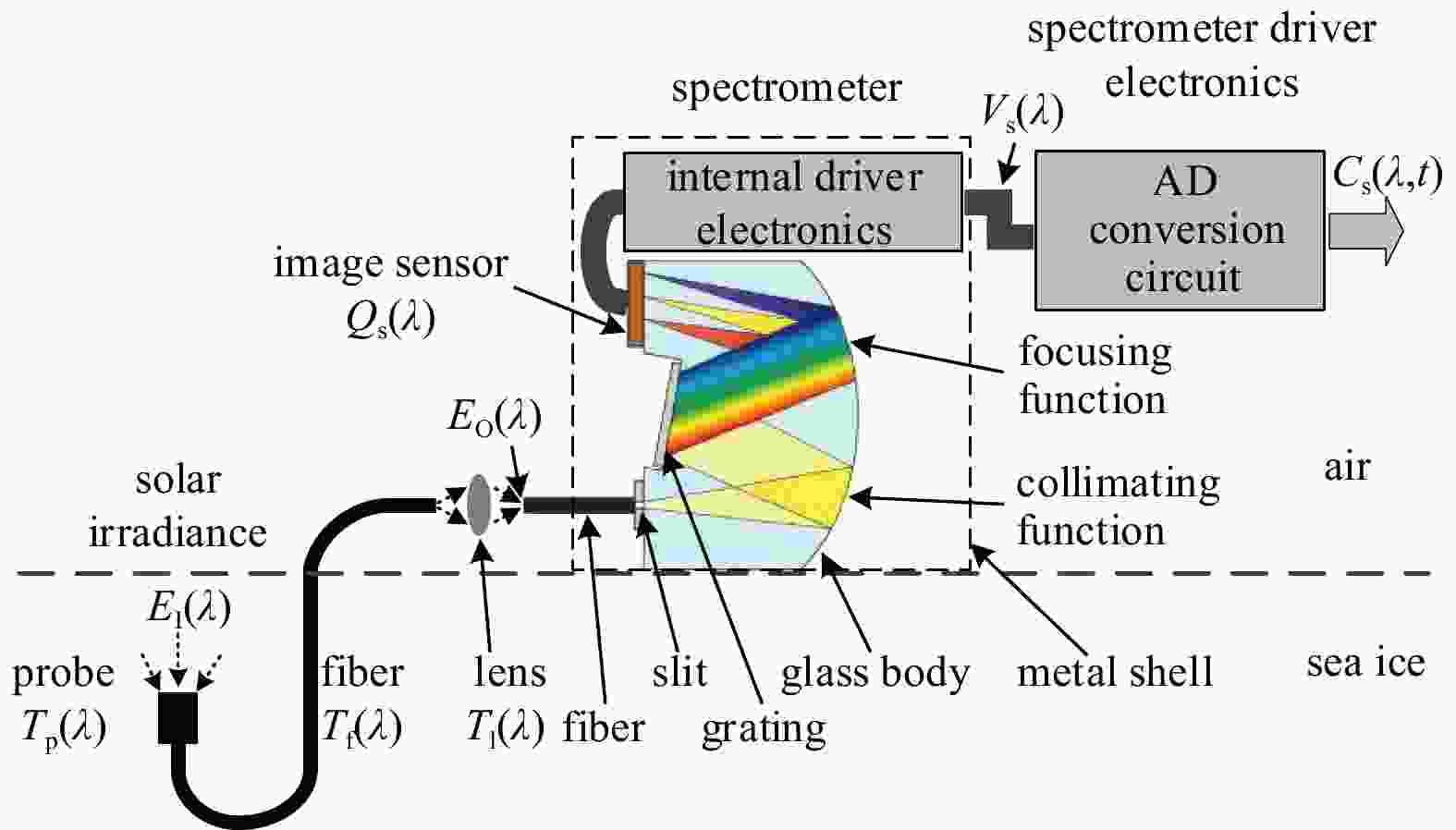
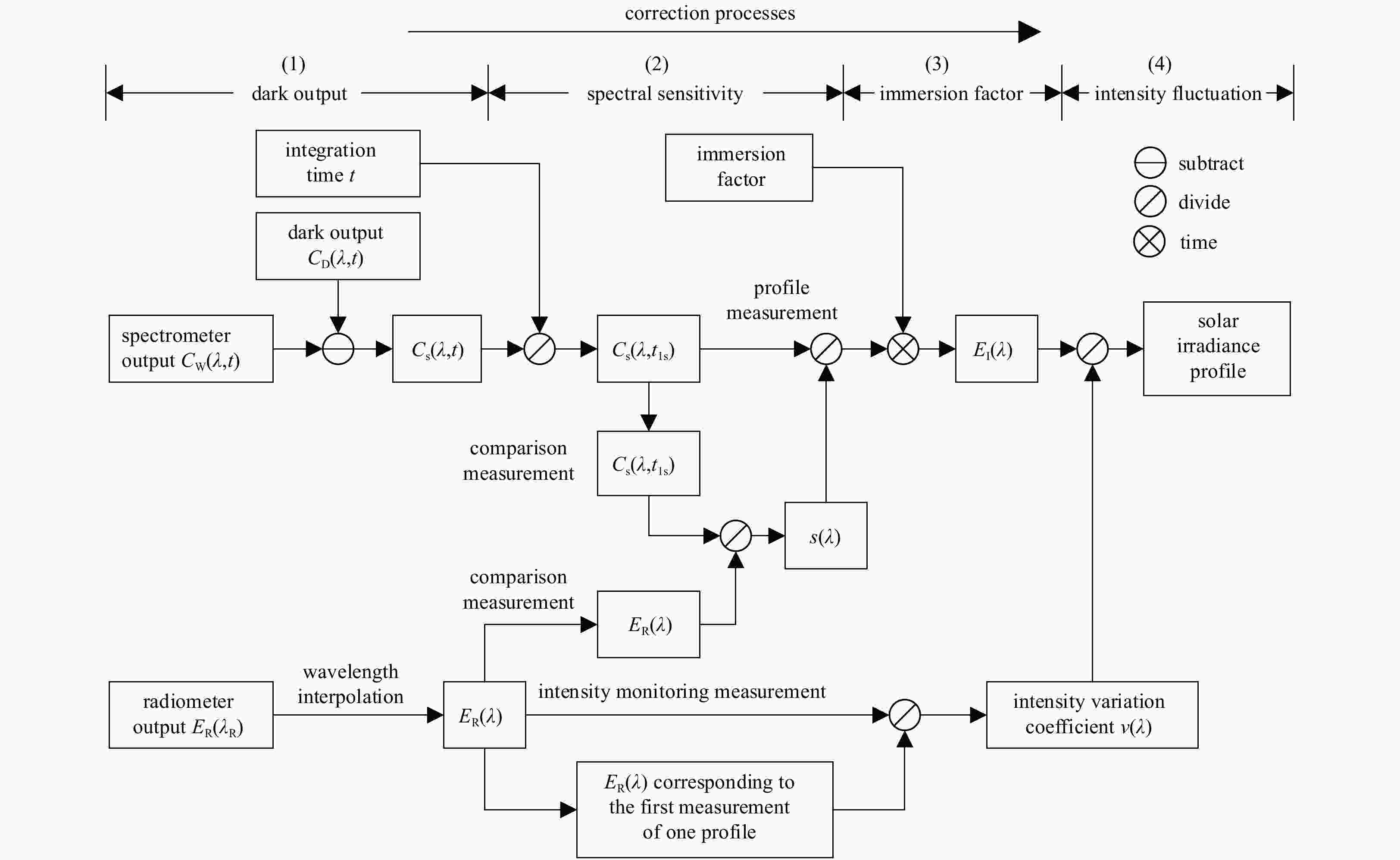
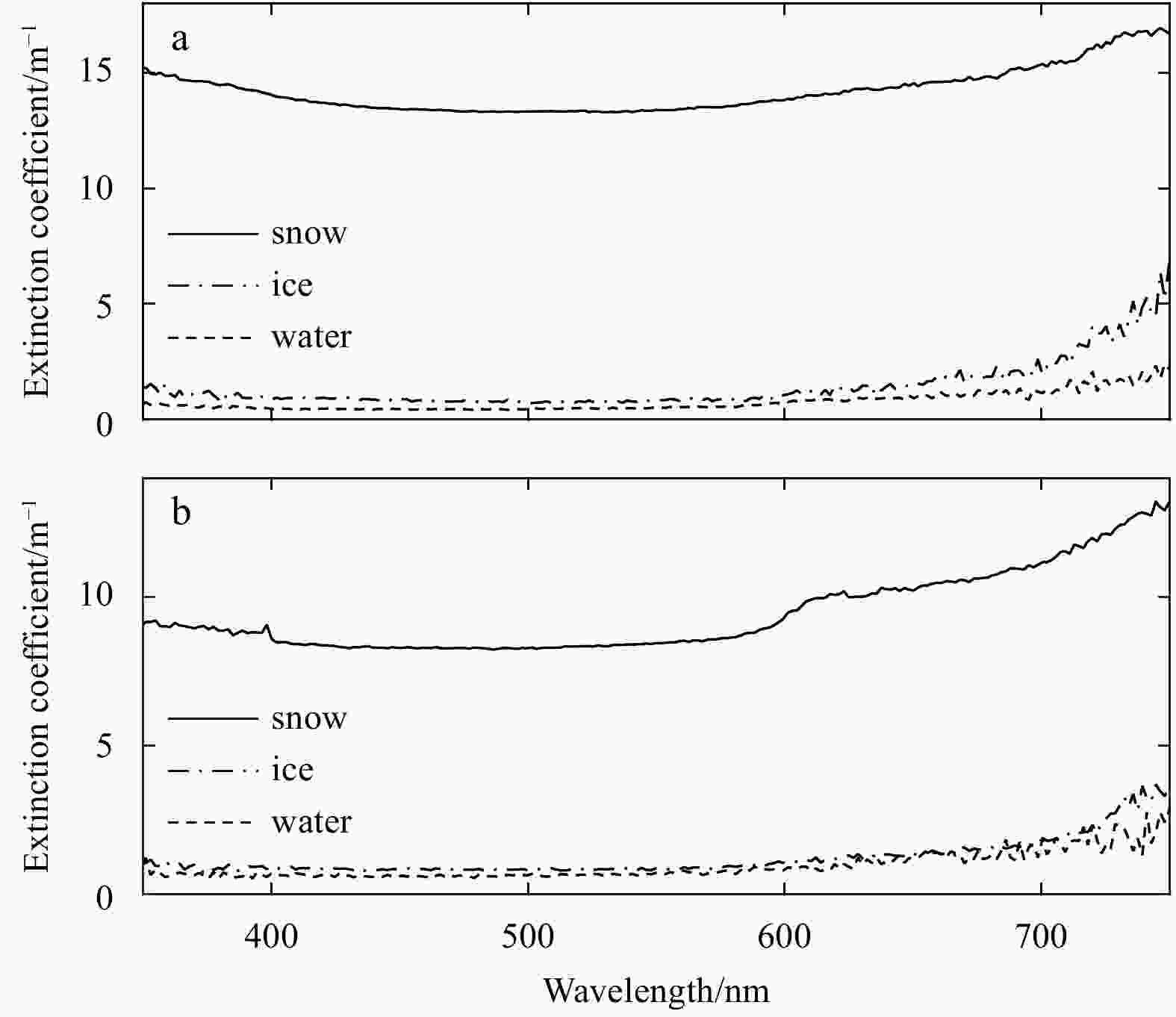
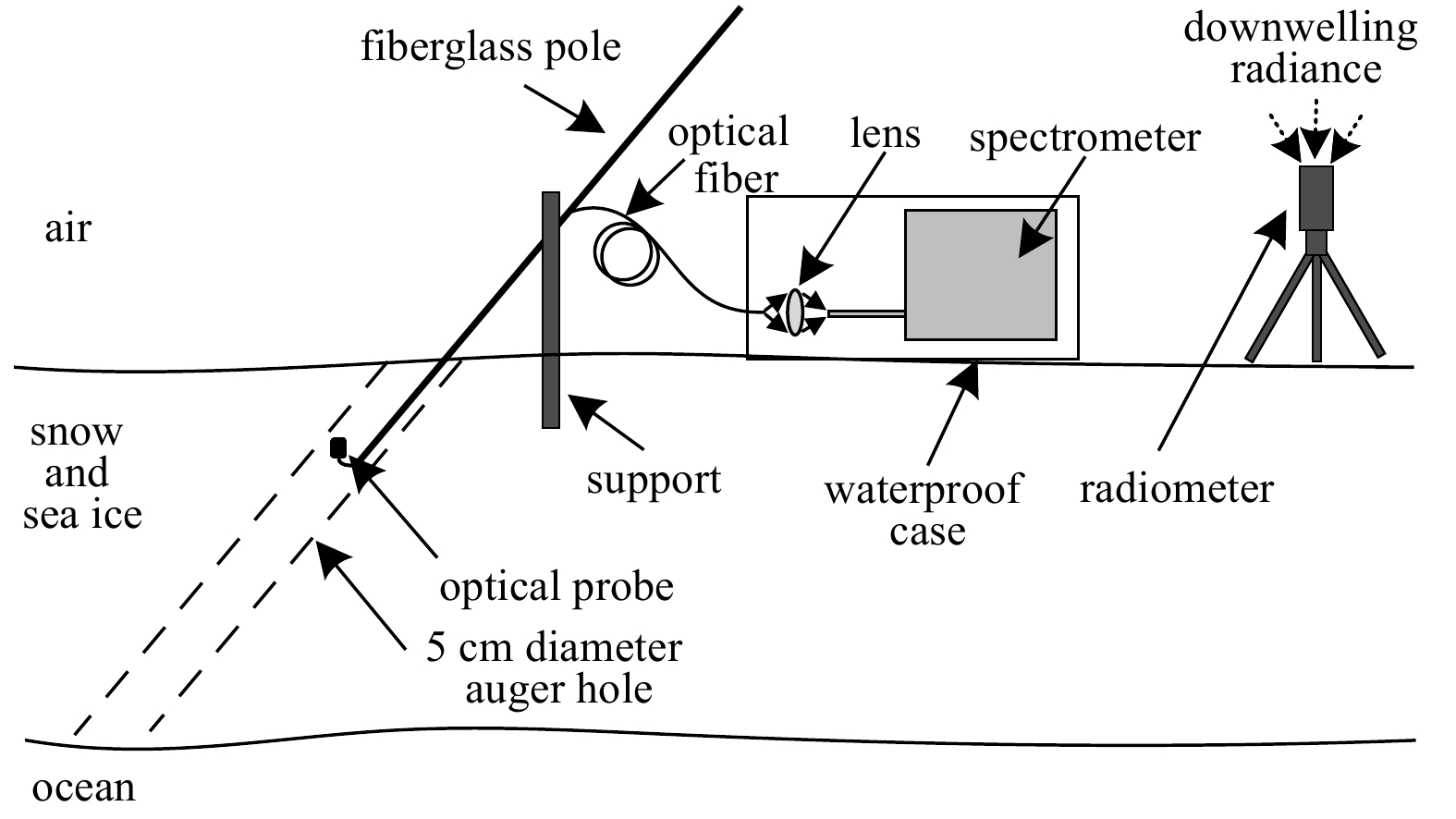
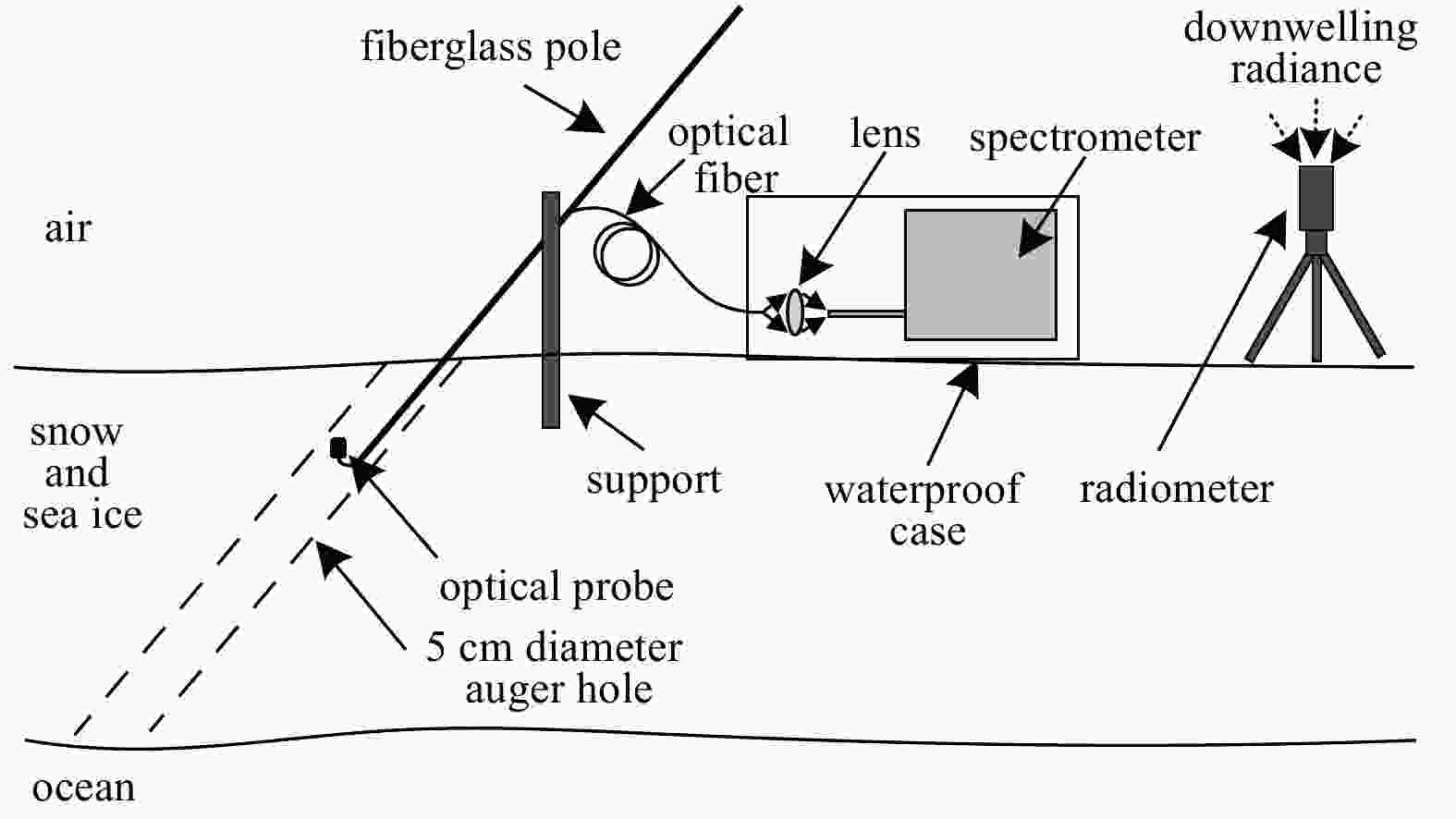
Measuring solar irradiance profiles in the Arctic sea ice using fiber optic spectrometry via inclined holes
-
Abstract: An irradiance profile measurement approach and profiling system were developed to measure the solar irradiance profile of the Arctic sea ice using fiber optic spectrometry. The approach involved using a miniature spectrometer to sense light signals collected and transmitted from a fiber probe. The fiber probe was small, and could thus move freely in inclined bore holes drilled in sea ice with its optical entrance pointing upward. The input-output relationship of the system was analyzed and built. Influence factors that determined the system output were analyzed. A correctional system output approach was proposed to correct the influence of these factors, and to obtain the solar irradiance profile based on the measurements outputted by this system. The overall performance of the system was examined in two ice floes in the Arctic during the 9th Chinese National Arctic Research Expedition. The measured solar irradiance profiles were in good agreement with those obtained using other commercially available oceanographic radiometers. The derived apparent optical properties of sea ice were comparable to those of similar sea ice measured by other optical instruments.
-
Key words:
- solar irradiance /
- profile /
- sea ice /
- fiber optic spectrometry /
- inclined hole
-
Figure 1. Schematic diagram of measurement site, including measurements of radiation above and within ice.
Figure 2. Schematic of the light signal transmission and conversion, from entering the optical probe to becoming the system output.
Figure 3. Schematic of the algorithm for correcting and calibrating the spectral measurement to obtain the solar irradiance profile in sea ice.
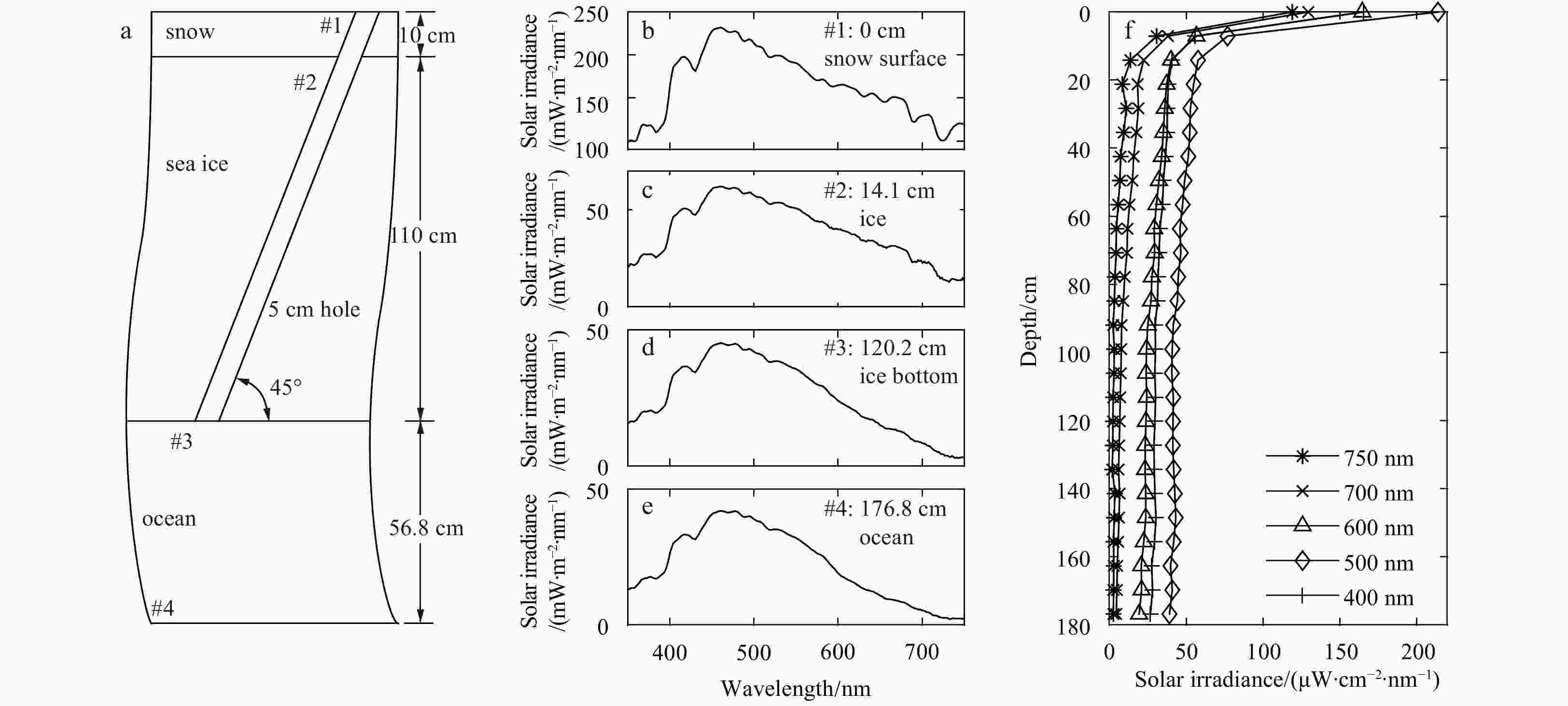
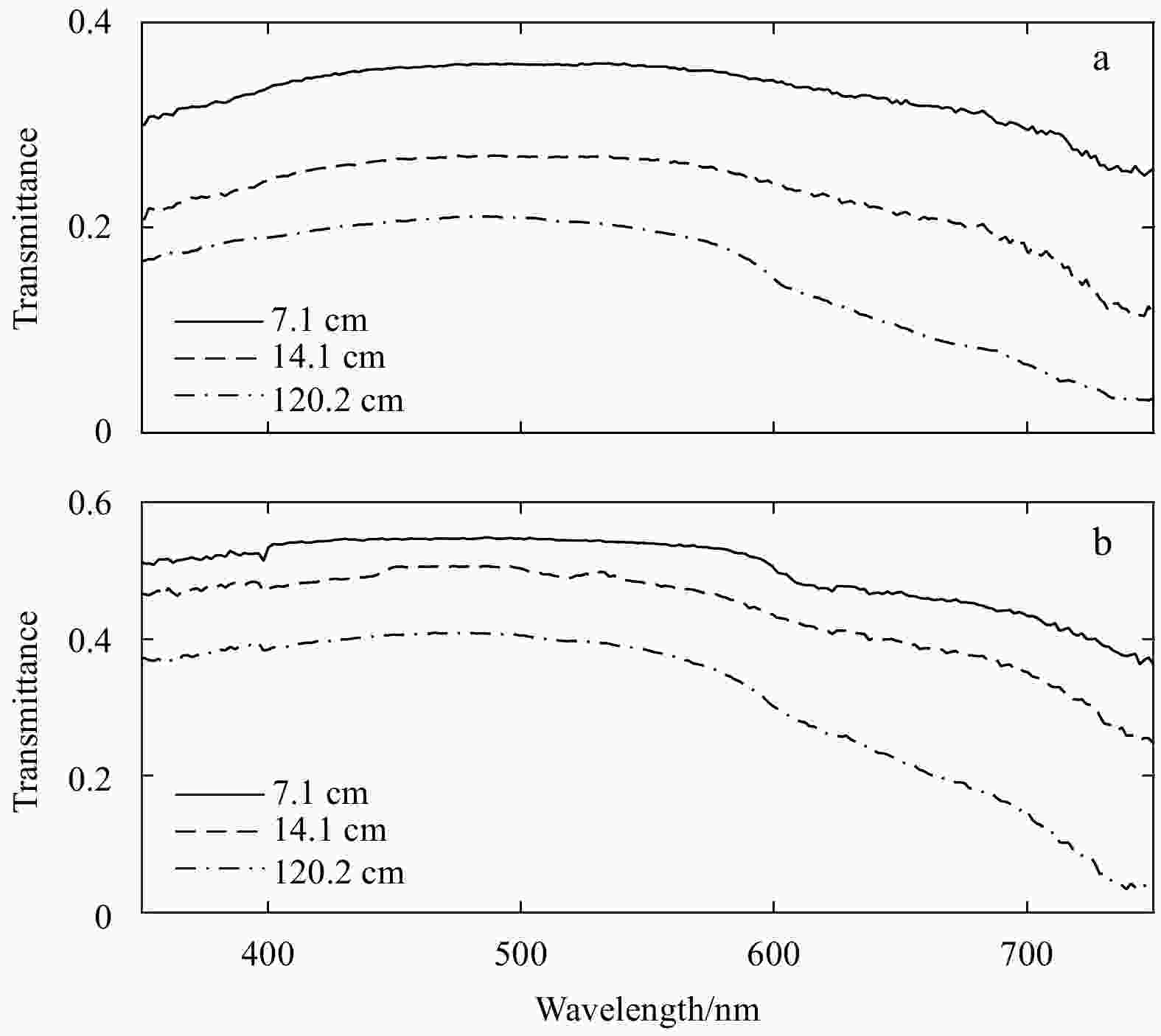
Figure 4. Overview sketch of the irradiance profile measurements, indicating the location of four demonstrative measurements #1–#4 (a), solar irradiance as a function of wavelength for locations #1–#4 ( b–e), and profiles of the solar irradiance for five selective wavelengths, extending from snow surface to the underlying ocean (f). This plot is derived from measurements collected at Site 1, which are very similar to those at Site 2.
Figure 5. Extinction coefficients of different media as a function of wavelength at Site 1 (a) and Site 2 (b).
Figure 6. Bulk attenuation coefficient of sea ice as a function of wavelength at the two measurement sites.
-
[1] Arrigo K R. 2014. Sea ice ecosystems. Annual Review of Marine Science, 6: 439–467. doi: 10.1146/annurev-marine-010213-135103 [2] Arrigo K R, Sullivan C W, Kremer J N. 1991. A bio-optical model of Antarctic sea ice. Journal of Geophysical Research: Oceans, 96(C6): 10581–10592. doi: 10.1029/91JC00455 [3] Arrigo K R, van Dijken G, Pabi S. 2008. Impact of a shrinking Arctic ice cover on marine primary production. Geophysical Research Letters, 35(19): L19603. doi: 10.1029/2008GL035028 [4] Ehn J K, Mundy C J, Barber D G. 2008a. Bio-optical and structural properties inferred from irradiance measurements within the bottommost layers in an Arctic landfast sea ice cover. Journal of Geophysical Research: Oceans, 113(C3): C03S03. doi: 10.1029/2007JC004194 [5] Ehn J K, Papakyriakou T N, Barber D G. 2008b. Inference of optical properties from radiation profiles within melting Landfast sea ice. Journal of Geophysical Research: Oceans, 113(C9): C09024. doi: 10.1029/2007JC004656 [6] Feister U, Grewe R. 1995. Spectral albedo measurements in the UV and visible region over different types of surfaces. Photochemistry and Photobiology, 62(4): 736–744. doi: 10.1111/j.1751-1097.1995.tb08723.x [7] Frey K E, Perovich D K, Light B. 2011. The spatial distribution of solar radiation under a melting Arctic sea ice cover. Geophysical Research Letters, 38(22): L22501. doi: 10.1029/2011GL049421 [8] Grenfell T C, Light B, Perovich D K. 2006. Spectral transmission and implications for the partitioning of shortwave radiation in arctic sea ice. Annals of Glaciology, 44: 1–6. doi: 10.3189/172756406781811763 [9] Grenfell T C, Maykut G A. 1977. The optical properties of ice and snow in the Arctic Basin. Journal of Glaciology, 18(80): 445–463. doi: 10.1017/S0022143000021122 [10] Grenfell T C, Perovich D K. 1984. Spectral albedos of sea ice and incident solar irradiance in the southern Beaufort Sea. Journal of Geophysical Research: Oceans, 89(C3): 3573–3580. doi: 10.1029/JC089iC03p03573 [11] Haas C, Thomas D N, Bareiss J. 2001. Surface properties and processes of perennial Antarctic sea ice in summer. Journal of Glaciology, 47(159): 613–625. doi: 10.3189/172756501781831864 [12] Lei Ruibo, Zhang Zhanhai, Matero I, et al. 2012. Reflection and transmission of irradiance by snow and sea ice in the central Arctic Ocean in summer 2010. Polar Research, 31(1): 17325. doi: 10.3402/polar.v31i0.17325 [13] Leu E, Mundy C J, Assmy P, et al. 2015. Arctic spring awakening-Steering principles behind the phenology of vernal ice algal blooms. Progress in Oceanography, 139: 151–170. doi: 10.1016/j.pocean.2015.07.012 [14] Light B, Grenfell T C, Perovich D K. 2008. Transmission and absorption of solar radiation by Arctic sea ice during the melt season. Journal of Geophysical Research: Oceans, 113(C3): C03023. doi: 10.1029/2006jc003977 [15] Light B, Perovich D K, Webster M A, et al. 2015. Optical properties of melting first-year Arctic sea ice. Journal of Geophysical Research: Oceans, 120(11): 7657–7675. doi: 10.1002/2015JC011163 [16] Maslanik J A, Fowler C, Stroeve J, et al. 2007. A younger, thinner Arctic ice cover: Increased potential for rapid, extensive sea-ice loss. Geophysical Research Letters, 34(24): L24501. doi: 10.1029/2007GL032043 [17] Mueller J L, Morel A, Frouin R, et al. 2003. Radiometric measurements and data analysis protocols. In: Mueller J L, Fargion G S, Mcdain C R, eds. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume III. Greenbelt, Maryland, USA: Goddard Space Flight Space Center, NASA/TM-2003-211621/Rev-Vol III [18] Nan Liwen, Wang Hangzhou, Han Jiwan, et al. 2017. Development and evaluation of a driver circuitry for miniature spectrometers used in cold environments. IEICE Electronics Express, 14(20): 20170876. doi: 10.1587/elex.14.20170876 [19] Nicolaus M, Gerland S, Hudson S R, et al. 2010a. Seasonality of spectral albedo and transmittance as observed in the Arctic Transpolar Drift in 2007. Journal of Geophysical Research: Oceans, 115(C11): C11011. doi: 10.1029/2009jc006074 [20] Nicolaus M, Hudson S R, Gerland S, et al. 2010b. A modern concept for autonomous and continuous measurements of spectral albedo and transmittance of sea ice. Cold Regions Science and Technology, 62(1): 14–28. doi: 10.1016/j.coldregions.2010.03.001 [21] Petzold T, Austin R W. 1988. Characterization of MER-1032. San Diego: University of California [22] Saenz B T, Arrigo K R. 2012. Simulation of a sea ice ecosystem using a hybrid model for slush layer desalination. Journal of Geophysical Research: Oceans, 117(C5): C05007. doi: 10.1029/2011JC007544 [23] Serreze M C, Holland M M, Stroeve J. 2007. Perspectives on the Arctic’s shrinking sea-ice cover. Science, 315(5818): 1533–1536. doi: 10.1126/science.1139426 [24] Thomas D N, Dieckmann G S. 2009. Sea Ice. 2nd ed. West Sussex: John Wiley and Sons [25] Vancoppenolle M, Meiners K M, Michel C, et al. 2013. Role of sea ice in global biogeochemical cycles: Emerging views and challenges. Quaternary Science Reviews, 79: 207–230. doi: 10.1016/j.quascirev.2013.04.011 [26] Wang Hangzhou, Nan Liwen, Huang Hui, et al. 2017. Adaptive measurement method for miniature spectrometers used in cold environments. Applied Optics, 56(28): 8029–8039. doi: 10.1364/AO.56.008029 [27] Wang Hangzhou, Song Hong, Chen Ying, et al. 2015. Correcting temperature dependence in miniature spectrometers used in cold polar environments. Applied Optics, 54(11): 3162–3172. doi: 10.1364/AO.54.003162 [28] Xu Zhantang, Yang Yuezhong, Sun Zhaohua, et al. 2012. In situ measurement of the solar radiance distribution within sea ice in Liaodong Bay, China. Cold Regions Science and Technology, 71: 23–33. doi: 10.1016/j.coldregions.2011.10.005 [29] Zhao Jinping, Li Tao. 2009. The solar radiation penetrating sea ice with very low solar altitude. Periodical of Ocean University of China (in Chinese), 39(5): 822–828 -
下载:
点击查看大图
图(7)
计量
- 文章访问数: 255
- HTML全文浏览量: 43
- PDF下载量: 13
- 被引次数: 0
