| Citation: | YANG Guang, HE Hailun, WANG Yuan, HAN Xiqiu, WANG Yejian. Evaluating a satellite-based sea surface temperature by shipboard survey in the Northwest Indian Ocean[J]. Acta Oceanologica Sinica, 2016, 35(11): 52-58. doi: 10.1007/s13131-016-0847-4 |
In meteorology and oceanography, variational data assimilation (VDA) uses all valuable observational information to achieve the most accurate description of atmospheric and oceanic states by minimizing the difference between model solutions and observations. The VDA includes three-dimensional VDA (3D-Var) and four-dimensional VDA (4D-Var) (Courtier, 1997; Wang et al., 2019b). Both 3D-Var and 4D-Var play an important role in numerical prediction, reanalysis data construction, parameter inversion and sensitivity analysis (Huang et al., 2005; Moore et al., 2011a, b; Zhang et al., 2017; Zhou et al., 2018; Shi et al., 2018; Wang et al., 2019a).
According to the difference in solution spaces, the 4D-Var can be divided into two kinds. One is solved in the model space, denoted
Despite the benefits mentioned above, 4D-PSAS is seldom adopted in the atmospheric and oceanic numerical models. While, P4D-Var is now widely used in the 4D-Var system of the European Centre for Medium-Range Weather Forecasts (ECMWF) (Rabier et al., 2000), National Centers for Environmental Prediction (NECP) (Parrish and Derber, 1992), Met Office (Rawlins et al., 2007), China Meteorological Administration (CMA), National Climate Center (NCC) (Liu et al., 2005) and other institutions, and its utility has been widely tested.
Recently, Moore et al. (2011a) develop the Regional Ocean Modeling System (ROMS). The ROMS contains its own 4D-Var system, which includes three modules: a primal formulation of incremental strong constraint 4D-Var (I4D-Var), a dual formulation based on a physical-space statistical analysis system (4D-PSAS), and a dual formulation representer-based variant of 4D-Var (R4D-Var). Since 4D-PSAS is seldom applied both in meteorology and in oceanography, the present paper utilizes the ROMS 4D-PSAS for data assimilation (DA) in the South China Sea. This paper is organized as follows: The ROMS and its 4D-Var systems are introduced in Section 2; Section 3 is the application of the ROMS 4D-Var systems in the South China Sea, and both P4D-Var and 4D-PSAS are carried out using the Conjugate gradient algorithm (CG) (Hestenes and Stiefel, 1952); Section 4 is the application of the Minimum residual algorithm (MINRES) (Paige and Saunders, 1975) in 4D-PSAS, and the comparison is made between the CG and MINRES algorithm; and finally, a summary is presented in Section 5.
The ROMS is developed by the Institute of Marine and Coastal Sciences of Rutgers University and the University of California, Los Angeles (Shchepetkin and McWilliams, 2005). It is a hydrostatic, primitive equation, Boussinesq ocean general circulation model, widely used in coastal, offshore and marine basins. ROMS uses terrain-following vertical coordinate system (S-coordinate), which allowing for greater vertical resolution in shallow water and regions with complex bathymetry, and can better simulate irregular continental shelf topography. Orthogonal curvilinear coordinates are used allowing for increased horizontal resolution in irregular coastal regions.
The ROMS 4D-Var system includes three modules: I4D-Var, 4D-PSAS and R4D-Var. For each module, ROMS can be used combined with available observations to yield a best estimate of the ocean state. In the primal formulation of I4D-Var the search for the best solution is performed in the full space of the model control vector, while for the dual formulations of 4D-PSAS and R4D-Var only the sub-space of linear functions of the model state vector spanned by the observations (i.e., the dual space) is searched. In oceanographic applications, the number of observations is typically much less than the dimension of the model control vector, and therefore there are remarkable advantages for performing search in the space spanned by the observations. For the completeness of the context and convenience of readers, I4D-Var (i.e., P4D-Var) and 4D-PSAS are summarized as follows.
In atmospheric and oceanic forecasting, when the model is assumed to be perfect (i.e., the model is error-free), the discrete atmospheric and oceanic numerical models can generally be expressed as follows:
| $${{{x}}_i} = {{{{\cal{M}}}}_{i,i - 1}}{{{x}}_{i - 1}},$$ | (1) |
where
4D-Var obtains the optimal estimation of the initial field by constructing a cost function
| $$\begin{split} {\cal{J}}\left({{{{x}}_0}} \right) =& \frac{1}{2}\left[{{{{x}}_0} - {{{x}}_{\rm{b}}},{{{B}}^{ - 1}}\left({{{{x}}_0} - {{{x}}_b}} \right)} \right] + \\ & \frac{1}{2}\sum\limits_{i = 0}^M {\left\langle {{{\cal{{{{{H}}}}}}_i}\left({{{{x}}_i}} \right) - {{{y}}_i},{{R}}_i^{ - 1}\left({{{\cal{{{{H}}}}}_i}\left({{{{x}}_i}} \right) - {{{y}}_i}} \right)} \right\rangle } = \min ! \end{split}, $$ | (2) |
where
The dimension of the state vector is very large, up to the order of 107–109. In order to reduce the computation cost, the incremental method is introduced to VDA by Courtier et al. (1994) through linearizing the nonlinear model and observation operator with respect to the model trajectory (Courtier et al., 1994):
| $$\left\{ {\begin{aligned} & {\Delta {{{x}}_i} = {{{M}}_{i,i - 1}}\Delta {{{x}}_{i - 1}},}\qquad\qquad{{{{M}}_{i,i - 1}} = {{\left. {\frac{{\partial {{{{\cal{M}}}}_{i,i - 1}}}}{{\partial x}}} \right|}_{{{x}} = {{{x}}_{\rm{b}}}}}} \\ & {{{{{\cal{H}}}}_i}\left({{{{x}}_i}} \right) = {{{{\cal{H}}}}_i}\left({{{{x}}_{\rm{b}}}} \right) + {{{H}}_i}\Delta {{{x}}_i},}\quad{{{{H}}_i} = {{\left. {\frac{{\partial {{{{\cal{H}}}}_i}}}{{\partial {{x}}}}} \right|}_{{{x}} = {{{x}}_{\rm{b}}}}}} \end{aligned}} \right.,$$ | (3) |
where
| $$\begin{split} \Delta {{{x}}_i} &= {{{M}}_{i,i - 1}}\Delta {{{x}}_{i - 1}} \\ & = {{{{M}}_{i,i - 1}} \cdot {{{M}}_{i - 1,i - 2}}\Delta {{{x}}_{i - 2}} = \! \cdot \!\cdot \! \cdot = {{{M}}_{i,0}}\Delta {{{x}}_0}} \end{split},$$ | (4) |
where
| $$J\left({\Delta {{{x}}_0}} \right) = \frac{1}{2}\left({\Delta {{{x}}_0},{{{B}}^{ - 1}}\Delta {{{x}}_0}} \right) + \frac{1}{2}\left\langle {{{G}}\Delta {{{x}}_0} - {{d}},{{{R}}^{ - 1}}\left({{{G}}\Delta {{{x}}_0} - {{d}}} \right)} \right\rangle,$$ | (5) |
where
For P4D-Var, the gradient of J is:
| $$\nabla J\left({\Delta {{{x}}_0}} \right) = \left({{{{B}}^{ - 1}} + {{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{G}}} \right)\Delta {{{x}}_0} - {{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{d}}.$$ | (6) |
According to
| $$\Delta {{x}}_0^a = {\left({{{{B}}^{ - 1}} + {{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{G}}} \right)^{ - 1}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{d}}.$$ | (7) |
In order to avoid the difficulty of inversion of B matrix and improve the condition number of Hessian matrix of cost function, the variable transformation,
| $$J\left({{v}} \right) = \frac{1}{2}\left({{{v}},{{v}}} \right) + \frac{1}{2}\left\langle {{{G}}{{{B}}^{1/2}}{{v}} - {{d}},{{{R}}^{ - 1}}\left({{{G}}{{{B}}^{1/2}}{{v}} - {{d}}} \right)} \right\rangle .$$ | (8) |
Then, the gradient and Hessian matrix of J with respect to v are:
| $${\nabla _v}J = \left({{{{I}}_n} + {{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{G}}{{{B}}^{1/2}}} \right){{v}} - {{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{d}},$$ | (9) |
| $$\nabla _v^2J = {{{I}}_n} + {{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{G}}{{{B}}^{1/2}},$$ | (10) |
where In is the unit matrix in the model space. The Hessian matrix refers to the second derivative of the cost function, which determines the properties of the cost function (Thépaut and Moll, 1990).
In order to turn P4D-Var into 4D-PSAS, the analytic solution of the minimization Eq. (7) is, using the Sherman-Morrison-Woodbury Formula
| $$\Delta {{x}}_0^a = {{B}}{{{G}}^{\rm{T}}}{\left({{{R}} + {{GB}}{{{G}}^{\rm{T}}}} \right)^{ - 1}}{{d}}.$$ | (11) |
To avoid the inversion of
| $$\left({{{R}} + {{GB}}{{{G}}^{\rm{T}}}} \right){{w}} = {{d}}.$$ | (12) |
Then, the solution w is transformed to the state vector increment in the model space,
Equation (12) is equivalent to a minimization problem of the following cost function F:
| $$F\left({{w}} \right) = \frac{1}{2}\left\langle {{{w}},\left({{{R}} + {{GB}}{{{G}}^{\rm{T}}}} \right){{w}}} \right\rangle - \left\langle {{{w}},{{d}}} \right\rangle,$$ | (13) |
which is usually called the auxiliary cost function in 4D-PSAS (defined in the observation space) so as to distinguish from the cost function J in P4D-Var (defined in the model space).
By making the variable transformation
| $$F\left({{u}} \right) = \frac{1}{2}\left\langle {{{u}},{{{R}}^{ - 1/2}}\left({{{R}} + {{GB}}{{{G}}^{\rm{T}}}} \right){{{R}}^{ - 1/2}}{{u}}} \right\rangle - \left\langle {{{u}},{{{R}}^{ - 1/2}}{{d}}} \right\rangle .$$ | (14) |
Then, the gradient and Hessian matrix of F with respect to u are:
| $${\nabla _{{u}}}F = \left({{{{I}}_m} + {{{R}}^{ - 1/2}}{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}} \right){{u}} - {{{R}}^{ - 1/2}}{{d}},$$ | (15) |
| $$\nabla _{{u}}^2J = {{{I}}_m} + {{{R}}^{ - 1/2}}{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}},$$ | (16) |
where Im is the unit matrix in the physical space.
Mapping the solution u of Eq. (14) in 4D-PSAS to the model space,
| $$\begin{split} {J_{\rm{p}}}\left({\tilde {{v}}} \right) =& \frac{1}{2}\left({\tilde {{v}},\tilde {{v}}} \right) + \frac{1}{2}\left\langle {{{G}}{{{B}}^{1/2}}\tilde {{v}} - {{d}},{{{R}}^{ - 1}}\left({{{G}}{{{B}}^{1/2}}\tilde {{v}} - {{d}}} \right)} \right\rangle \\ =& \frac{1}{2}\left( {{{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}{{u}},{{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}{{u}}} \right) +\\ & \frac{1}{2}\left\langle {{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}{{u}} - {{d}},{{{R}}^{ - 1}}\left( {{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}{{u}} - {{d}}} \right)} \right\rangle . \end{split} $$ | (17) |
The Hessian matrices of J and F are:
| $$\nabla _{{v}}^2J \equiv {{V}} = {{{I}}_n} + {{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{G}}{{{B}}^{1/2}},$$ | (18) |
| $$\nabla _{{u}}^2F \equiv {{U}} = {{{I}}_m} + {{{R}}^{ - 1/2}}{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}.$$ | (19) |
Suppose that the eigenvalue and eigenvector of V is
| $$\left({{{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1}}{{G}}{{{B}}^{1/2}}} \right){{{V}}_i} = \left({{\lambda _i} - 1} \right){{{V}}_i},$$ | (20) |
| $$\left({{{{R}}^{ - 1/2}}{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}} \right){{{U}}_i} = \left({{\varLambda _i} - 1} \right){{{U}}_i}.$$ | (21) |
Let
| $$\begin{split} &{\left({{{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}} \right)^{ - 1}}\left({{{{B}}^{1/2}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}} \right)\left({{{{R}}^{ - 1/2}}{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}} \right){{{U}}_i} \\ &= \left({{\lambda _i} - 1} \right){{{U}}_i}. \end{split}$$ | (22) |
In the special case m=n, V and U have the same eigenvalue, i.e.,
The ROMS 4D-Var system is now applied to the case of South China Sea, and the observational data are temperature profile and sea surface temperature. Both P4D-Var and 4D-PSAS are fulfilled and the analysis field by P4D-Var is regarded as a reference. The assimilation utility of 4D-PSAS is analyzed according to the cost function curves and the increment fields obtained by the assimilation. The optimal algorithm used in P4D-Var and 4D-PSAS is the CG algorithm (Moore et al., 2011c).
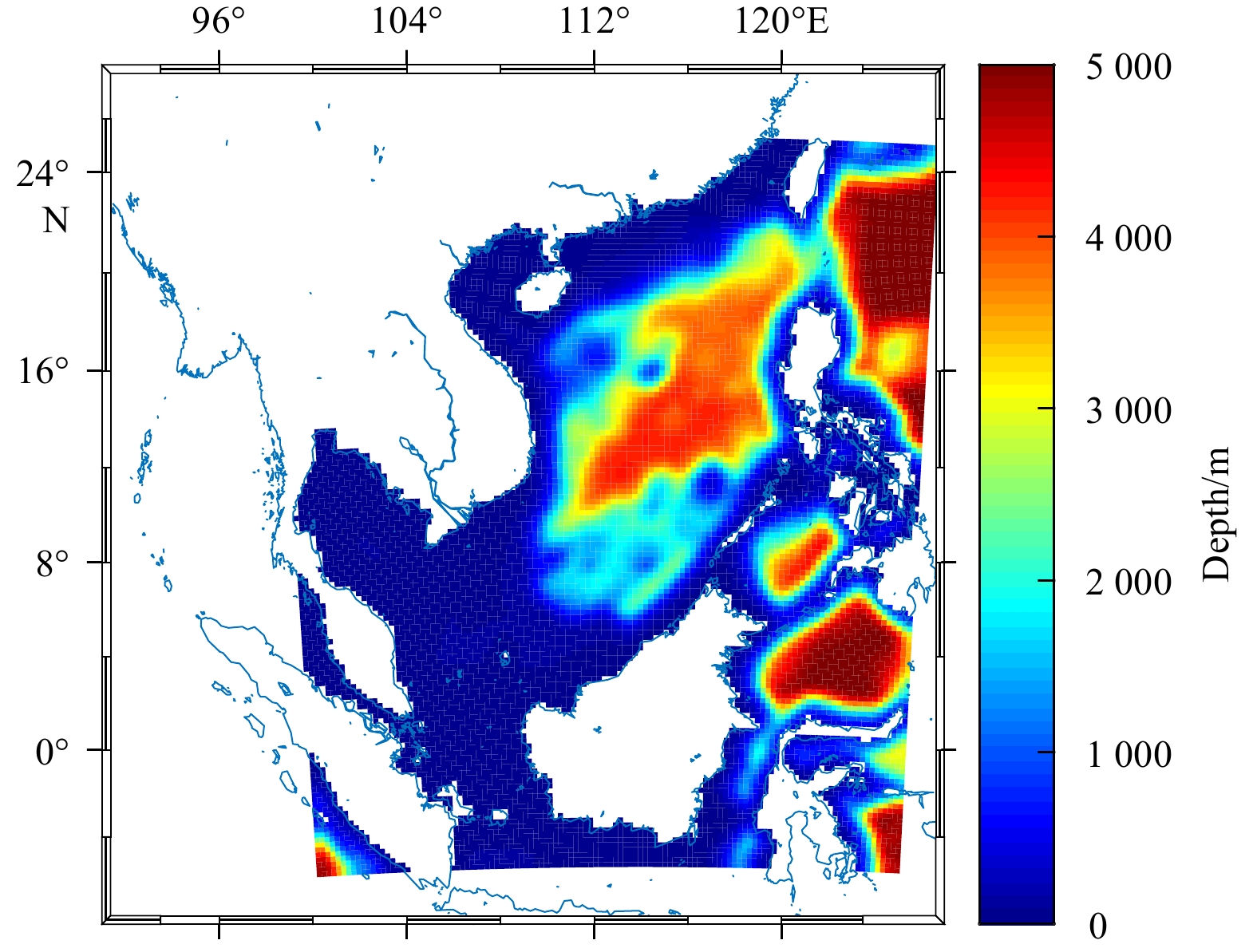
The model domain covers the South China Sea and its adjacent waters (5.44°S–25.36°N, 98.05°–126.73°E). Figure 1 shows the topographic depth in the model domain, provided by the ETOPO1 data (Amante and Eakins, 2009). The maximum depth is set to 5 km, with a horizontal resolution of (1/4)°×(1/4)° and 32 S-coordinate layers in the vertical. The stretching parameters of S-coordinate are set to
This paper chooses the ocean reanalysis data of Hybrid Coordinate Ocean Model (HYCOM) in the model domain at 00:00 on February 1, 2012 as the initial field (Shu et al., 2014) and NCEP reanalysis data as the forcing field (Amenu and Kumar, 2005). Firstly, the spin up process is carried out, and the model runs for a model year to obtain a stable state of the ocean. The model output field at 00:00 on February 1, 2013 was used as the initial field for DA experiment. The assimilation window was 4 d and the number of iterations was set at 50 times. The observations used is a blend of data from the version 4 of the Met Office Hadley Centre EN series of data sets (EN4) (Good et al., 2013) and the sea surface temperature data of the National Oceanic and Atmospheric Administration (NOAA) (Lauritson, 1991) in the assimilation window. The EN4 data set is a set of global quality-controlled ocean temperature and salinity profiles collected, processed and released by the Met Office Hadley Centre. Sea surface temperature data, the daily and grid product, is provided by the National Climatic Data Center (NCDC) of NOAA.
Figure 2 shows the dependence of
Figures 3a and b show the sea surface temperature increments (i.e., the deviation between the analysis field and the background field) obtained after the 50th iteration of P4D-Var and 4D-PSAS, respectively. It can be found that the increments obtained by 4D-PSAS and P4D-Var are largely identical when cost functions reach complete convergence after 50 iterations, and the average relative deviation between them is only 0.28% and the root mean square error (RMSE) is 0.50 K.
Figures 3c and d show the sea surface temperature increments obtained after the 10th iteration of P4D-Var and 4D-PSAS, respectively. It can be seen that there are obvious differences, with an average relative deviation of 24.63% and a RMSE is 0.85 K. This shows that the solutions obtained using 4D-PSAS and P4D-Var are, in general, very different if the iterations are terminated before the asymptote in cost functions have been reached.
The difference in cost functions between 4D-PSAS and P4D-Var is analyzed firstly from the physical sense. The cost function J of P4D-Var derives from the posterior probability density function, which represents the analysis error. Decrease in J means increase in accuracy of analysis solutions, so iterations in P4D-Var ensures that the analysis solutions are more and more accurate. However, for 4D-PSAS, the auxiliary cost function F has no direct physical meaning, and the iteration solution is often undesirable until the cost function achieves its minimum.
On the other hand, at the point of minimum of F,
| $${{{u}}^{\rm{a}}} = {\left({{{{I}}_m} + {{{R}}^{ - 1/2}}{{GB}}{{{G}}^{\rm{T}}}{{{R}}^{ - 1/2}}} \right)^{ - 1}}{{{R}}^{ - 1/2}}{{d}}.$$ | (23) |
At
| $$F\left({{{{u}}^{\rm{a}}}} \right) = - \frac{1}{2}\left\langle {{{{u}}^{\rm{a}}},{{{R}}^{ - 1/2}}{{d}}} \right\rangle .$$ | (24) |
Through the variable transformations,
| $$J\left({\Delta {{{x}}_0}} \right) = \frac{1}{2}\left\langle {{{{u}}^{\rm{a}}},{{{R}}^{ - 1/2}}{{d}}} \right\rangle \equiv - F\left({{{{u}}^{\rm{a}}}} \right).$$ | (25) |
From Eq. (25), it is obvious that when the cost functions reach their minimum, J(v) and F(u) are of opposite sign. Since the analysis solution in P4D-Var is determined directly by minimizing the cost function J(v), while in 4D-PSAS is determined indirectly by minimizing the auxiliary cost function F(u). Therefore, the equivalence between 4D-PSAS and P4D-Var can only guarantee the similarity in convergence of F(u) and of J(v), but cannot guarantee that between
Next, we will analyze the relationship between the cost function Jp and auxiliary cost function F. According to Eq. (17), using
| $$\begin{split} {J_{\rm{p}}}\left({{\tilde{ v}}} \right) =& \frac{1}{2}{{{u}}^{\rm{T}}}{{L}}{{{L}}^{\rm{T}}}{{u}} + \frac{1}{2}{{{u}}^{\rm{T}}}{{L}}{{{L}}^{\rm{T}}}{{L}}{{{L}}^{\rm{T}}}{{u}} - {{{u}}^{\rm{T}}}{{L}}{{{L}}^{\rm{T}}}{{{R}}^{ - 1/2}}{{d}} + \frac{1}{2}{{{d}}^{\rm{T}}}{{{R}}^{ - 1}}{{d}} \\ =& \frac{1}{2}{{{u}}^{\rm{T}}}{{L}}\left({{{{I}}_n} + {{{L}}^{\rm{T}}}{{L}}} \right){L^{\rm{T}}}{{u}} - {{{u}}^{\rm{T}}}{{L}}{{{L}}^{\rm{T}}}{{d}}' + \frac{1}{2}{{d}}{'^{\rm{T}}}{{d}}' \\ =& \frac{1}{2}{{{u}}^{\rm{T}}}\left({{{{I}}_m} + {{L}}{{{L}}^{\rm{T}}}} \right){{L}}{{{L}}^{\rm{T}}}{{u}} - {{{u}}^{\rm{T}}}{{L}}{{{L}}^{\rm{T}}}{{d}}' + \frac{1}{2}{{d}}{'^{\rm{T}}}{{d}}' ,\\[-15pt] \end{split} $$ | (26) |
where
Similarly, according to Eq. (14), using the L operator, F can be written as:
| $$F\left({{u}} \right) = \frac{1}{2}{{{u}}^{\rm{T}}}\left({{{{I}}_m} + {{L}}{{{L}}^{\rm{T}}}} \right){{u}} - {{{u}}^{\rm{T}}}{{d}}'.$$ | (27) |
Rearranging terms, Eq. (26) can be rewritten as:
| $$\begin{split} {J_{\rm{p}}}\left({{\tilde{ v}}} \right) =& \frac{1}{2}{\left[ {\left({{{{I}}_m} + {{L}}{{{L}}^{\rm{T}}}} \right){{u}} - {{d}}'} \right]^{\rm{T}}}\left[ {\left({{{{I}}_m} + {{L}}{{{L}}^{\rm{T}}}} \right){{u}} - {{d}}'} \right] - \\ & {\frac{1}{2}{{{u}}^{\rm{T}}}\left({{{{I}}_m} + {{L}}{{{L}}^{\rm{T}}}} \right){{u}} + {{d}}{'^{\rm{T}}}{{u}}} . \end{split} $$ | (28) |
Using Eqs (27) and (28), the relationship between Jp and F is:
| $${J_{\rm{p}}}\left({{\tilde{ v}}} \right) = \frac{1}{2}{\left\| {{\nabla _u}F} \right\|^2} - F\left({{u}} \right).$$ | (29) |
According to Eq. (29), when F is mapped from the physical space to Jp in the model space, Jp is related not only to F itself, but also to the norm of gradient of F.
Figure 4 shows the dependence of the gradient norm
By analyzing the principle of optimization algorithm, this paper explores the causes of oscillation of the gradient norm. In the following section, the feasibility of improving the convergence property of 4D-PSAS using the MINRES algorithm, which guarantees the monotonic reduction of residual error, is studied, and its effect is verified by numerical experiments.
Here, for brevity of contents, more about the CG and MINRES algorithms are attached as an appendix. The CG algorithm is applied to solving Eq. (A11) and an approximate solution is found by minimizing the A norm of the absolute error.
| $${{{x}}_l} = {\left\| {{{x}} - {{{x}}_*}} \right\|_A} = \mathop {\min !}\limits_{{{x}} \in {{{x}}_0} + {{\cal{K}}^l}} .$$ | (30) |
As stated in Appendix,
Unlike the CG algorithm, the MINRES algorithm is applied to solving Eq. (A14), and an approximate solution is found by minimizing the residual norm.
| $${{{x}}_l} = {\left\| {{{b}} - {{Ax}}} \right\|_2} = \mathop {\min !}\limits_{{{x}} \in {{{x}}_0} + {{\cal{K}}^l}} .$$ | (31) |
According to recursive relation Eq. (A16),
The improvement of 4D-PSAS using MINRES algorithm is tested from three aspects: gradient norm curves, cost function curves and increment fields. The experiment configuration is consistent with Section 2.4.1.
Figure 5 shows the dependence of the gradient norm on number of iterations in 4D-PSAS. As can be seen from Fig. 5, the gradient norm obtained by the MINRES algorithm decreases significantly compared with the CG algorithm, and the oscillation phenomenon disappears during the iteration process.
Figure 6 shows the dependence of

From Fig. 6, it seems that the convergence in P4D-Var/CG is better than that in 4D-PSAS/MINRES. But in fact, the two schemes are for different spaces, the model space and physical space. Usually, the model space and physical space differ by the order 102 in dimension, so the computation time for the two schemes should also be considered for comparison. As shown in Fig. 7, the relationship is given between the cost function and computer time over the time interval from 10 000 s to 18 000 s, and it should be noted that the number of iterations for the three experiments were all set to 50, so the three curve were stooped at different time. It can be seen that the final time at complete convergence in 4D-PSAS is about 3 000–4 000 s earlier than that in P4D-Var, which reduce the running time by roughly 12 % in assimilation.
Figure 8 shows the sea surface temperature increments obtained after 10 iterations of assimilation experiments. Figure 8a is the increment obtained by P4D-Var, and the optimization algorithm used in the iteration is CG algorithm; Figs 8b and c are the increments obtained by 4D-PSAS, and the optimization algorithms used in the iteration are CG algorithm and MINRES algorithm, respectively.
After using MINRES algorithm, we can see that the increment obtained by 4D-PSAS/MINRES are improved significantly. Compared with results of Section 2.4.2, The average relative deviation between the increment fields of 4D-PSAS and P4D-Var is reduced from 24.63% to 5.04%, and the RMSE is reduced from 0.85 K to 0.19 K. This shows that MINRES algorithm can effectively improve the assimilation results of 4D-PSAS during the iteration process.
In this paper, the ROMS 4D-Var system is applied to data assimilation of South China Sea, and two kinds of schemes, P4D-Var (in the model space) and 4D-PSAS (in the observation space) modules are performed. Theoretically, the 4D-PSAS data assimilation scheme is superior to the P4D-Var scheme. However, when the CG algorithm is employed in P4D-Var and 4D-PSAS respectively, the iteration processes exhibit different characteristics. Although the effective convergence of the cost functions is reached both in P4D-Var and in 4D-PSAS, the behaviors of the cost functions, J and Jp, are different. Obviously, J decreases monotonically, while Jp shows fluctuational property, and the convergence rate of Jp is obviously slower than that of J. In addition, the average relative deviation between the sea surface temperature increments obtained using P4D-Var and 4D-PSAS is 24.63% after the 10th iteration. The non-monotonic reduction of Jp is found to be due to the non-monotonic variation of the gradient norm of the auxiliary cost function F in 4D-PSAS. In order to suppress the non-monotonic variation of the gradient norm of Jp during the iteration process, the CG algorithm is replaced by the MINRES algorithm in 4D-PSAS. The data assimilation experiments indicate that the cost function Jp of 4D-PSAS decreases monotonically and the convergence rate clearly increases. And, the sea surface temperature increment obtained by 4D-PSAS after 10th iteration is basically consistent with that of P4D-Var, and the average relative deviation between the sea surface temperature increments obtained by 4D-PSAS and P4D-Var is reduced from 24.63% to 5.04%.
To sum up, the MINRES algorithm can not only guarantee monotonic reduction of the gradient norm of the cost function Jp in 4D-PSAS, but also can significantly improve the convergence property of the iteration process.
|
Bell M M, Montgomery M T, Emanuel K A. 2012. Air-sea enthalpy and momentum exchange at major hurricane wind speeds observed during CBLAST. J Atmos Sci, 69:3197-3222
|
|
Burkill P H, Mantoura R F C, Owens N J P. 1993. Biogeochemical cycling in the northwestern Indian Ocean:a brief overview. Deep-Sea Res 40(3):643-649
|
|
Chen Dake, Lian Tao, Fu Congbin, et al. 2015. Strong influence of westerly wind bursts on El Niño diversity. Nat Geosci, 8:339-345
|
|
Dong C M, Nencioli F, Liu Y, et al. 2011. An automated approach to detect oceanic eddies from satellite remotely sensed sea surface temperature data. IEEE Geoscience and Remote Sensing Letters, 8(6):1055-1059
|
|
Donlon C J, Casey K S, Robinson I S, et al. 2009. The GODAE high-resolution sea surface temperature pilot project. Oceanography, 22:34-45
|
|
Donlon C J, Martin M, Stark J, et al. 2012. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sensing of Environment, 116:140-158
|
|
Donlon C J, Minnett P J, Gentemann C, et al. 2002. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J Climate, 15:353-369
|
|
Gentemann C L. 2014. Three way validation of MODIS and AMSR-E sea surface temperatures. J Geophys Res, 119:2583-2598
|
|
Gentemann C L, Wentz F J, Mears C A, et al. 2004. in situ validation of tropical rainfall measuring mission microwave sea surface temperatures. Journal of Geophysical Research, 109:C04021
|
|
Hu Haibo, Hong Xiaoyuan, Zhang Yuan, et al. 2013. The critical role of Indian summer monsoon on the remote forcing between Indian and Northwest Pacific during El Niño decaying year. Sci China:Earth Sci, 56(3):408-417
|
|
Lian Tao, Chen Dake, Tang Youmin, et al. 2014. Effects of westerly wind bursts on El Niño:a new perspective. Geophys Res Lett, 41(10):3522-3527
|
|
Liu Xiaohui, Chen Dake, Dong Changming, et al. 2016. Variation of the Kuroshio intrusion pathways northeast of Taiwan using the Lagrangian method. Sci China:Earth Sci, 59:268-280
|
|
Liu Xiaohui, Dong Changming, Chen Dake, et al. 2014. The pattern and variability of winter Kuroshio intrusion northeast of Taiwan. J Geophys Res, 119:5380-5394
|
|
O'Carroll A G, August T, Le Borgne P, et al. 2012. The accuracy of SST retrievals from METOP-A IASI and AVHRR using the EUMETSAT OSI-SAF matchup dataset. Remote Sensing of Environment, 126:184-194
|
|
O'Carroll A G, Eyre J R, Saunders R W. 2008. Three-way error analysis between AATSR, AMSR-E, and in situ sea surface temperature observations. J Atmos Oceanic Technol, 25(7):1197-1207
|
|
Parekh A, Sharma R, Sarkar A. 2007. A comparative assessment of surface wind speed and sea surface temperature over the Indian Ocean by TMI, MSMR, and ERA-40. J Atmos Oceanic Technol, 24:1131-1142
|
|
Park K A, Chung J Y, Kim K, et al. 1994. A study on comparison of satellite-tracked drifter temperature with satellite-derived sea surface temperature of NOAA/NESDIS. Korean J Remote Sens, 10(2):83-107
|
|
Park K A, Chung J Y, Kim K, et al. 1999. Sea surface temperature retrievals optimized to the East Sea (Sea of Japan) using NOAA/AVHRR data. Marine Technology Society Journal, 33(1):23-35
|
|
Park K A, Lee E Y, Chung S R, et al. 2011. Accuracy assessment of sea surface temperature from NOAA/AVHRR data in the seas around Korea and error characteristics. Korean J Remote Sens, 27(6):663-675
|
|
Qiu C H, Wang D X, Kawamura H, et al. 2009. Validation of AVHRR and TMI-derived sea surface temperature in the northern South China Sea. Cont Shelf Res, 29(20):2358-2366
|
|
Reynolds R W. 1993. Impact of mount Pinatubo aerosols on satellitederived sea surface temperatures. J Climate, 6:768-774
|
|
Reynolds R W, Gentemann C L, Corlett G K. 2010. Evaluation of AATSR and TMI satellite SST data. J Climate, 23(1):152-165
|
|
Senan R, Anith S, Sengupta D. 2001. Validation of SST and WS from TRMM Using North Indian Ocean Moored Buoy Observations. CAOS Report 2001AS1, Centre for Atmospheric and Oceanic Sciences, Indian Institute of Science, Bangalore, Indian
|
|
Stark J D, Donlon C J, Martin M J, et al. 2007. OSTIA:an operational, high resolution, real time, global sea surface temperature analysis system. In OCEANS 2007. Marine challenges:coastline to deep sea. Aberdeen:IEEE Ocean Engineering Society, 331-334, doi:10.1109/OCEANSE. 2007. 4302251
|
|
Udaya B T V S, Rahman S H, Pavan I D, et al. 2009. Comparison of AMSR-E and TMI sea surface temperature with Argo near-surface temperature over the Indian Ocean. Int J Remote Sens, 30:2669-2684
|
|
Walton C C. 1988. Nonlinear multichannel algorithms for estimating sea surface temperature with AVHRR satellite data. J Appl Meteor, 27:115-124
|
|
Wentz F J, Gentemann C, Smith D, et al. 2000. Satellite measurements of sea surface temperature through clouds. Science, 288(5467):847-850
|
|
Williams G N, Zaidman P C, Glembocki N G, et al. 2014. Comparison between remotely-sensed sea-surface temperature (AVHRR) and in situ records in San Matías Gulf (Patagonia, Argentina). Latin American Journal of Aquatic Research, 42(1):192-203
|
|
Wu Qiaoyan, Yan Ying, Chen Dake. 2013. A linear Markov model for East Asian monsoon seasonal forecast. Journal of Climate, 26:5183-5195
|
|
Wu Qiaoyan, Yan Ying, Chen Dake. 2016. Seasonal prediction of East Asian monsoon precipitation:skill sensitivity to various climate variabilities. Int J Climatol, 36:324-333
|