| Citation: | Mingliang Zhang, Yongpeng Ji, Yini Wang, Hongxing Zhang, Tianping Xu. Numerical investigation on tsunami wave mitigation on forest sloping beach[J]. Acta Oceanologica Sinica, 2020, 39(1): 130-140. doi: 10.1007/s13131-019-1527-y |
Tsunamis are giant waves in the ocean, which are generally generated by marine earthquakes, underwater volcanic eruptions, or submerged landslides in the deep sea. They propagate from the deep sea to the coastline with vast losses to life and property, destruction of critical infrastructure in low-lying coastal areas, and massive damage to the coastal ecosystem (such as the Indian Ocean tsunami in 2004, Samoa tsunami in 2009, Chile tsunami in 2010, and Tohoku tsunami in 2011) (Ulvrová et al., 2014). These great threats of tsunami waves in coastal regions demonstrate the necessity of building artificial obstacles to mitigate the hazardous effects caused by tsunamis. The shallow water equations(SWEs) can usually be used to describe wave propagation in the ocean; the need in wavelength of water wave is much longer than the water depth (Wu et al., 2016). Vreugdenhil (1994) concluded that the SWEs provided a roughly reasonable model in simulating tsunami propagation. With advances in numerical simulation technology and methodology, several types of numerical models have been conducted to investigate the wave propagation processes and tsunami run-up heights in coastal waters. Typical models were considered, including depth-integrated shallow water models (SWM) (Liu et al., 2009; Kanayama and Dan, 2013; Vater et al., 2015) and Boussinesq-type models (Iimura and Tanaka, 2012; Touhami and Khellaf, 2017). A tsunami is a kind of long wave found in the ocean. Results show that SWM are more robust and efficient for tsunami predictions in experimental cases and real-scale basins than those of Boussinesq-type models. Three methods of FVM, finite element method (FEM), and finite difference method (FDM) coupled with SWE were frequently applied for simulating wave propagation, breaking, run-up, and land inundation (Li and Raichlen, 2002; Lotto and Dunham, 2015; Takase et al., 2016). When waves pass over the sloping beach, where the discontinuous flows occur in the process of wave run-up and run-down, it brings about challenges for some models in treating the dry-wet interface for the moving coastline. Godunov-type schemes based on a Riemann solver had remarkable shock-capturing capabilities, often being used to reproduce the process of wave propagation and coastal hazard modeling. It has been demonstrated that these schemes are attractive methods in treating the wet/dry front during run-up and discontinuous flows (Kazolea and Delis, 2013; Liang et al., 2015).
It is well known that native vegetation growing on coastal beaches is regarded as a means of providing stabilization to coastal banks (Blackmar et al., 2014). Furthermore, they can also function as a natural barrier against catastrophic storm surges or tsunamis by attenuating wave energy in sloping coastal beaches (Kathiresan and Rajendran, 2005; Yao et al., 2018). Taking tsunamis as an example, as they pass through the coastal vegetation, the wave energy is significantly dissipated as a result of reducing tsunami disasters. Therefore, the mechanics of vegetation in protecting coastal regions against tsunami hazards have become a hot topic of research in recent years. Further, numerical models have been widely applied in helping to understand the interactions between tsunami waves and estuarine vegetations. Tang et al. (2013) used the nonlinear shallow water model to reproduce long wave run-up on sloping beaches in the presence of rigid vegetation for small scale experimental cases. Iimura and Tanaka (2012) developed a depth-averaged non-linear long-wave model to test the ability of coastal forest in reducing tsunami damage. Real-scale simulations of tsunami waves were generated to investigate the effectiveness of forests as a bio-shield, with the results indicating that forests of Pandanus odoratissimus and Casuarina equisetifolia were effective for increasing drag and mitigating tsunami disaster in coastal zones (Thuy et al., 2012). Tanaka (2009) pointed out that P. odoratissimus was especially effective in providing protection from tsunami damage because of its density and complex aerial root structure. In marine or estuarine wetlands, there are many factors impacting tsunami energy attenuation including bed friction, vegetation types, forest density, drag force caused by vegetation with complex leaf shapes, as well as rigid and flexible properties. Generally speaking, a limited number of reports and literature discuss the interaction mechanics between impacting factors with tsunami waves. Accordingly, related questions are worthy of further exploration.
In this paper, we numerically investigate the hydrodynamic processes on a vegetated sloping beach and quantify the effects of vegetation on the wave run-up by solving a one-dimensional model. The proposed model is validated for non-breaking solitary wave propagating on a bare sloping beach, and then the periodic long wave propagating on vegetation sloping beach is simulated to examine the computation accuracy of the numerical model. Finally, the model is applied to calculate tsunami wave propagation on an actual-scale forest-covered beach to study the possible effects of variable parameters on tsunami mitigation.
The one-dimensional numerical model is based on the SWEs, and they can be expressed in vector form as follows (Maleki and Khan, 2016):
| $${{D}}{{{U}}_t} + {{{F}}_x} = {{S}},$$ | (1) |
where t is the time; while U, F and S are the vectors of conserved variables, fluxes, and source term, respectively. It can be defined as follows:
| $$ \begin{split} { D} = & \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right],\;{ U} = \left[ {\begin{array}{*{20}{c}} h \\ {hu} \end{array}} \right],\;{ F} = \left[ {\begin{array}{*{20}{c}} {hu} \\ {huu} \end{array}} \right],\\ { S} = & \left[ {\begin{array}{*{20}{c}} 0 \\ {gh\dfrac{{\partial \eta }}{{\partial x}} - g{n^2}u\left| u \right|{h^{1/3}} - f} \end{array}} \right], \end{split} $$ | (2) |
where h is the flow depth, η is the water surface elevation, u is the depth-averaged velocity, g is the gravitational acceleration, n is the Manning roughness coefficient, and f is the vegetation effect force on the wave.
This numerical model uses a one-dimensional explicit FVM to solve the equations, which can be integrated at a control volume:
| $$\int_\Omega {{{D}}\frac{{\partial {{U}}}}{{\partial t}}} + \int_\Omega {\frac{{\partial {{F}}}}{{\partial x}}{\rm{d}}\Omega } = \int_\Omega {{{S}}{\rm{d}}\Omega }. $$ | (3) |
After discretizing, Eq. (3) becomes
| $$ \begin{split} U_i^{t + 1} = & U_i^t - \frac{{\Delta t}}{{\Delta {x_i}}}\left[ {F{{\left(U \right)}_{i + 1/2}} - F{{\left(U \right)}_{i - 1/2}}} \right]+ \\ & \Delta t\left[ {gh\Delta \eta _i^t - g{n^2}u_i^t\left| {u_i^t} \right|{{\left({h_i^t} \right)}^{1/3}} - f} \right]. \end{split} $$ | (4) |
where
The HLL approximate Riemann solver is a suitable choice to handle discontinuous solutions. It is used to determine the fluid mass and momentum fluxes at an interface as:
| $${F_{\rm {HLL}}} = \left\{ {\begin{array}{*{20}{c}} {{F_{\rm L}}} \\ {{F^*}} \\ {{F_{\rm R}}} \end{array}} \right.\begin{array}{*{20}{c}} {}&{{\rm {if}}\begin{array}{*{20}{c}} {{S_{\rm L}} \geqslant 0,}&{} \end{array}}&{} \\ {}&{\begin{array}{*{20}{c}} {}&{} \end{array}{\rm {if}}\begin{array}{*{20}{c}} {{S_{\rm L}} < 0 < {S_{\rm R}}},&{} \end{array}}&{} \\ {}&{{\rm {if}}\begin{array}{*{20}{c}} {{S_{\rm R}} \leqslant 0,}&{} \end{array}}&{} \end{array}$$ | (5) |
where
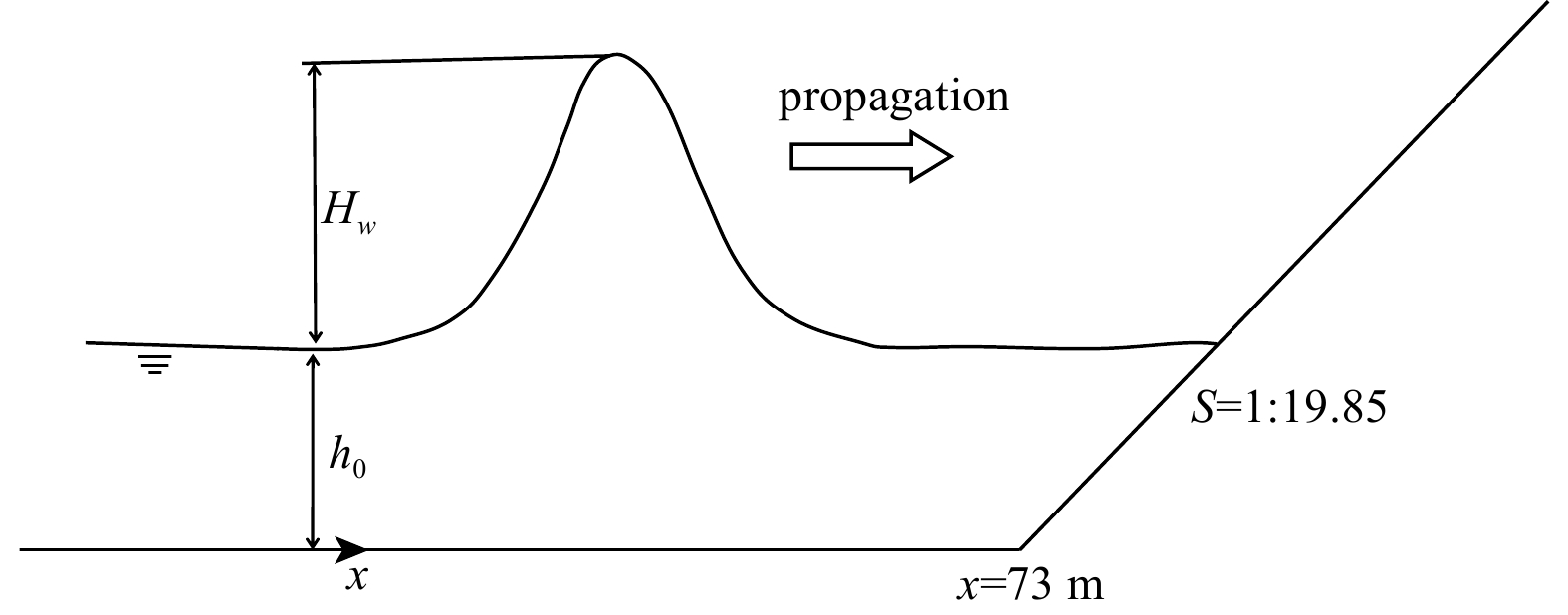
Solitary wave is one type of long wave, and it can propagate long distances without changes in wave characteristics (Tang et al., 2017). When it reaches the sloping beach, the wave run-up and run-down play an important role in the nearshore dynamics and sediment transport, which have attracted an increasing amount of attention in long-wave modeling. Synolakis (1986) carried out a series of laboratory experiments to investigate the non-breaking wave propagation on sloping beach, as shown in Fig. 1. In Synolakis’s experiment, the constant water depth was 1 m, solitary wave propagated from left to right on a 1:19.85 sloping beach, and its height was 0.018 5 m. In the present numerical experiment, the space step is 0.1 m, the Manning coefficient is 0.01, and the variable time step is needed to require a Courant-Friedrichs-Lewy (CFL) condition. Figure 2 shows the comparison between simulated results and experimental data in wave run-up and run-down for non-breaking solitary wave. For data analysis, we employed dimensionless time, length, and wave height. The water depth normalizes the wave height and length scale, while the time scale is normalized as
A laboratory experiment was conducted in Saitama University to explore the propagation of long periodic waves on a vegetation sloping beach (Thuy et al., 2018). In this experiment, the wave tank was 15 m long and 0.4 m wide, and the bed terrain consisted of various slopes (S =1:25, 1:4.7, and 1:20.5), as depicted in Fig. 3. The still water depth was 0.44 m. The vegetation diameter was 0.005 m, the vegetation density was 2 200 stem/m2, and the vegetation zone ranged from x = 10.36 to 11.36 m, as shown in Fig. 3. The drag coefficient CD of the vegetation was calibrated as 2.5 in the present case. An incident sinusoidal wave with a period of T = 20 s and wave height of 0.16 cm was implemented at the right boundary. In the present simulation case, the grid spacing is 0.01 m, the Manning coefficient is 0.012, and the time step is restricted by means of a Courant number of 0.7. Figure 4 compares the time series of velocities behind the vegetation, the simulated results in flow velocity are in agreement with the measured values, indicating that the a drag force from vegetation coupled with the momentum equation is reasonable for expressing the resistance effect on wave propagation.
Coastal vegetations growing on sloping beaches can act as a biological buffer zone, effectively reducing the tsunami run-up and mitigating natural disasters in coastal areas caused by tsunamis. A number of studies have emphasized the potential of coastal vegetation as a buffer zone to reduce damage caused by tsunamis (Tanaka, 2009; Thuy et al., 2010). As shown in Fig. 5, a coastal topography including four slopes (S = 1/10, 1/100, 1/50 and 1/500) was designed to investigate the impact of forests on tsunami wave propagation. The incident tsunami wave was represented in this work by a single sinusoidal wave with wave height of 6 m and wave period of 1 200 s, coming from the left side of open sea (Thuy et al., 2010). The still water depth was 100 m below the datum level, the tide level at the attack of the tsunami was considered to be 2 m. As shown in Fig. 5, the coastal vegetation was planted at the sloping beach with a slope of 1/500, where the ground was 4 m above the datum level (Thuy et al., 2010). The coastal forest was P. odoratissimus vegetation with complex aerial root structure. In the presence of forest cases, the tree height was 8 m, the reference diameter was 0.195 m, the vegetation density was 0.226 trees/m2, and the vegetation width was 100 m. The drag force coefficient of P. odoratissimus varied with water depth and was derived from field investigation (Tanaka, 2009). In this study, the computational domain is subdivided into uniform meshes with a size of 5 m, the time interval is 0.01 s, and the bottom roughness coefficient is 0.025. The tsunami force (F) is an important factor for the evaluation of the impact characteristics of tsunami, and it is defined and assessed as the following equation (Thuy et al., 2018):
| $${F} = \frac{1}{2}\rho hu\left| u \right|,$$ | (6) |
where ρ is water density, and u is calculated from present model.
Figure 6 shows the spatial distributions of maximum water level of the first run-up wave in the absence and presence of forest. In front of the vegetation domain, the water level with forest is significantly higher than that without forest, the water level drops more dramatically in the forest zone and maintains a lower water level behind the forest compared to that in absence of forest. Figure 7 shows the simulated results of water depth, current speed, and tsunami force in front of and behind forest zone for the non-vegetation case. Except for time delay, these results indicate that there are no significant differences in magnitude for the three variables in two locations (before forest and behind forest). Figure 8 shows the comparison of the simulated variables for the non-vegetated and vegetated cases. The numerical results indicate that the reflection and attenuation effect from the coastal forest on water depth is remarkable. The current speed and tsunami force dramatically reduce because of the vegetation resistance effect; the tsunami forces behind the vegetated domain decline by 75% compared to the simulated results in the absence of forest. These results show that this forest in a sloping beach environment can significantly reduce energy from tsunami waves, having an obvious effect of mitigating the natural disasters caused by tsunami waves.
Vegetation density is an important factor influencing tsunami wave attenuation in coastal beach covered with forest. In this numerical experiment, six different vegetation densities (0.1, 0.15, 0.2, 0.226, 0.3, and 0.35 tree/m2) are designed to investigate the interaction mechanism between coastal vegetation and tsunamis. Figure 9 shows the results comparing the front and back of the vegetated domain. In front of the forest domain, an increasing trend of water depth with rise of vegetation density is presented, but it is precisely the opposite behind the vegetated area. Compared to that in front of the vegetation zone, the maximum velocity behind the vegetation domain sharply declines with the rise of vegetation density. The tsunami force in front of and behind the vegetated area significantly decrease with rise of vegetation density, these conclusions can also be confirmed in Fig. 10. The conclusion can be drawn that the increase in vegetation density can more effectively mitigate the damage caused by the tsunami.
Seven wave heights (1.5, 2, 2.5, 3, 3.5, 4, and 4.5 m) are also selected to investigate the effect of coastal forest on tsunami wave mitigation. As shown in Fig. 11, we compare the differences in water depth, current speed, and tsunami force in different conditions of wave heights. Whether in front of the forest or behind it, three variables increase with an increase of wave height from 1.5 m to 4.5 m. Further, their maximum amplitude reaches ahead of time – the current speed and tsunami force in front of forest belt become steeper. As can be observed in Fig. 12, the maximum water depth and velocity behind the forest are noticeably smaller than those in front of the forest belt under condition of different wave heights, signifying that the presence of vegetation significantly contributes to the energy attenuation of tsunami waves. In addition, the increase of maximum depth and velocity with increasing wave height is seemingly linear in front of and behind the forest; the maximum value of tsunami force represents a nonlinear change with increasing incident wave height. In Fig. 13, as the wave periods (10, 20, 30, 40, and 50 min) increase, the maximum values for three variables in front of and behind the vegetated area are significantly delayed. Six sets of different Manning coefficients (0.01, 0.015, 0.02, 0.025, 0.03, and 0.035) are established in this numerical experiment.. The simulated results are shown in Fig. 14, water depth in front of forest decreases as the increasing of the Manning coefficient, while it increases behind forest. In the meanwhile, other variables in velocity and tsunami force decrease in front of and behind of vegetation area. In Fig. 15, the maximum water depth in front of the vegetation belt monotonously decreases with the increasing Manning coefficients, but there is a slightly increase behind the vegetation belt, the reductions of velocity and tsunami force are obvious in front of and behind of forest. The results indicate that the increment in Manning coefficients can more effectively mitigate the damage caused by the tsunami. Furthermore, in this simulation, three different slopes – typical (1:500), mild (1:250), and relatively steep (1:100) – extending from the shoreline were selected to identify the wave propagation on the topography variations with forest coverage. The simulated results are provided in Fig. 16. It can be observed that when the bed slope increases the maximum values for water depth, current velocity and tsunami force are almost steady in front of the forest, allowing them to clearly decrease behind the forest as the bed slope increases. It was determined that the slope effect (or gravitational effect) is a significant factor impacting tsunami energy dissipation on a sloping vegetation beach.
A FVM scheme of a one-dimensional model was presented in this work to simulate tsunami wave mitigation on a vegetated beach. The model was validated against two laboratory scale tests in predicting wave propagation processes for the non-breaking solitary wave and sine wave, it was then applied to reproduce the tsunami mitigation process when taking into consideration a forest effect. Numerical results matched well with the experimental measurement and available data in a real scale case. Some of the results can be summarized as follows:
(1) The proposed model has the capability of predicting wave run-up and run-down for solitary waves on a sloping beach, especially in treating dry-wet problems for moving shorelines.
(2) The vegetation on coastal beaches are effective in reducing energy loss for periodic long waves, implying that the drag force caused by vegetation as a source term into momentum equation is reliable for expressing the vegetation resistance in simulating wave propagation.
(3) The model reasonably predicts tsunami wave propagation in a series of cases where there is complex and real vegetation in a sloping beach. It is found that the vegetation belt in a sloping beach can reduce water depth, current speed, and tsunami force, effectively mitigating the damage caused by the tsunami.
(4) In addition to bed resistance and forest density, the parameters for tsunami wave height and wave period significantly impact wave energy attenuation on a vegetated beach. Furthermore, when the topography slope becomes steep, the reduction of three variables behind the forest is reduced on the sloping forest beach.
| [1] |
Blackmar P J, Cox D T, Wu Weicheng. 2014. Laboratory observations and numerical simulations of wave height attenuation in heterogeneous vegetation. Journal of Waterway, Port, Coastal, and Ocean Engineering, 140(1): 56–65. doi: 10.1061/(ASCE)WW.1943-5460.0000215
|
| [2] |
Iimura K, Tanaka N. 2012. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Engineering, 54: 223–232. doi: 10.1016/j.oceaneng.2012.07.025
|
| [3] |
Kanayama H, Dan H. 2013. A tsunami simulation of Hakata Bay using the viscous shallow-water equations. Japan Journal of Industrial and Applied Mathematics, 30(3): 605–624. doi: 10.1007/s13160-013-0111-7
|
| [4] |
Kathiresan K, Rajendran N. 2005. Coastal mangrove forests mitigated tsunami. Estuarine, Coastal and Shelf Science, 65(3): 601–606. doi: 10.1016/j.ecss.2005.06.022
|
| [5] |
Kazolea M, Delis A I. 2013. A well-balanced shock-capturing hybrid finite volume-finite difference numerical scheme for extended 1D Boussinesq models. Applied Numerical Mathematics, 67: 167–186. doi: 10.1016/j.apnum.2011.07.003
|
| [6] |
Kuiry S N, Wu Weiming, Ding Yan. 2012. A one-dimensional shock-capturing model for long wave run-up on sloping beaches. Journal of Hydraulic Engineering, 18(2): 65–79. doi: 10.1080/09715010.2012.662429
|
| [7] |
Li Ying, Raichlen F. 2002. Non-breaking and breaking solitary wave run-up. Journal of Fluid Mechanics, 456: 295–318. doi: 10.1017/S0022112001007625
|
| [8] |
Liang Qiuhua, Hou Jingming, Amouzgar R. 2015. Simulation of tsunami propagation using adaptive cartesian grids. Coastal Engineering Journal, 57(4): 1550016–1
|
| [9] |
Liu Yingchun, Shi Yaolin, Yuen D A, et al. 2009. Comparison of linear and nonlinear shallow wave water equations applied to tsunami waves over the China Sea. Acta Geotechnica, 4(2): 129–137. doi: 10.1007/s11440-008-0073-0
|
| [10] |
Lotto G C, Dunham E M. 2015. High-order finite difference modeling of tsunami generation in a compressible ocean from offshore earthquakes. Computational Geosciences, 19(2): 327–340. doi: 10.1007/s10596-015-9472-0
|
| [11] |
Maleki F S, Khan A A. 2016. 1-D coupled non-equilibrium sediment transport modeling for unsteady flows in the discontinuous Galerkin framework. Journal of Hydrodynamics, 28(4): 534–543. doi: 10.1016/S1001-6058(16)60658-3
|
| [12] |
Synolakis C E. 1986. The runup of long waves[dissertation]. Pasadena, CA: California Institute of Technology
|
| [13] |
Takase S, Moriguchi S, Terada K, et al. 2016. 2D-3D hybrid stabilized finite element method for tsunami runup Simulations. Computational Mechanics, 58(3): 411–422. doi: 10.1007/s00466-016-1300-4
|
| [14] |
Tanaka N. 2009. Vegetation bioshields for tsunami mitigation: review of effectiveness, limitations, construction, and sustainable management. Landscape and Ecological Engineering, 5(1): 71–79. doi: 10.1007/s11355-008-0058-z
|
| [15] |
Tang Jun, Causon D, Mingham C, et al. 2013. Numerical study of vegetation damping effects on solitary wave run-up using the nonlinear shallow water equations. Coastal Engineering, 75: 21–28. doi: 10.1016/j.coastaleng.2013.01.002
|
| [16] |
Tang Jun, Shen Yongming, Causon D M, et al. 2017. Numerical study of periodic long wave run-up on a rigid vegetation sloping beach. Coastal Engineering, 121: 158–166. doi: 10.1016/j.coastaleng.2016.12.004
|
| [17] |
Thuy N B, Nandasena N A K, Dang V H, et al. 2018. Simplified formulae for designing coastal forest against tsunami run-up: one-dimensional approach. Natural Hazards, 92(1): 327–346. doi: 10.1007/s11069-018-3197-z
|
| [18] |
Thuy N B, Tanaka N, Tanimoto K. 2012. Tsunami mitigation by coastal vegetation considering the effect of tree breaking. Journal of Coastal Conservation, 16(1): 111–121. doi: 10.1007/s11852-011-0179-7
|
| [19] |
Thuy N B, Tanimoto K, Tanaka N. 2010. Flow and potential force due to runup tsunami around a coastal forest with a gap-experiments and numerical simulations. Science of Tsunami Hazards, 29(2): 43–69
|
| [20] |
Touhami H E, Khellaf M C. 2017. Laboratory study on effects of submerged obstacles on tsunami wave and run-up. Natural Hazards, 87(2): 757–771. doi: 10.1007/s11069-017-2791-9
|
| [21] |
Ulvrová M, Paris R, Kelfoun K, et al. 2014. Numerical simulations of tsunamis generated by underwater volcanic explosions at Karymskoye lake (Kamchatka, Russia) and Kolumbo volcano (Aegean Sea, Greece). Natural Hazards and Earth System Sciences, 14(2): 401–412. doi: 10.5194/nhess-14-401-2014
|
| [22] |
Vater S, Beisiegel N, Behrens J. 2015. A limiter-based well-balanced discontinuous Galerkin method for shallow-water flows with wetting and drying: one-dimensional case. Advances in Water Resources, 85: 1–13. doi: 10.1016/j.advwatres.2015.08.008
|
| [23] |
Vreugdenhil C B. 1994. Numerical Methods for Shallow-water Flow. Dordrecht: Springer
|
| [24] |
Wu Guoxiang, Shi Fengyan, Kirby J T, et al. 2016. A pre-storage, subgrid model for simulating flooding and draining processes in salt marshes. Coastal Engineering, 108: 65–78. doi: 10.1016/j.coastaleng.2015.11.008
|
| [25] |
Yao Yu, Tang Zhengjiang, Jiang Changbo, et al. 2018. Boussinesq modeling of solitary wave run-up reduction by emergent vegetation on a sloping beach. Journal of Hydro-environment Research, 19: 78–87. doi: 10.1016/j.jher.2018.03.001
|
| [26] |
Zhang Mingliang, Hao Zining, Zhang Yunpeng, et al. 2013. Numerical simulation of solitary and random wave propagation through vegetation based on VOF method. Acta Oceanologica Sinica, 32(7): 38–46. doi: 10.1007/s13131-013-0330-4
|
| 1. | Hany Qoshirotur Rif’atin, Ikha Magdalena, Widjo Kongko, et al. Experimental and numerical evaluation of tsunami wave reduction through the implementation of sea dikes and trenches. IOP Conference Series: Earth and Environmental Science, 2025, 1464(1): 012008. doi:10.1088/1755-1315/1464/1/012008 | |
| 2. | Umberto De Maio, Fabrizio Greco, Paolo Lonetti, et al. A Multiscale Model to Assess Bridge Vulnerability Under Extreme Wave Loading. Journal of Marine Science and Engineering, 2024, 12(12): 2145. doi:10.3390/jmse12122145 | |
| 3. | Yanxu Wang, Zegao Yin, Quanlin Qiu, et al. Numerical study of wave run-up on sea dikes with vegetated foreshores. Physics of Fluids, 2024, 36(5) doi:10.1063/5.0204252 | |
| 4. | N. S. Abdelrahman, M. S. Abou-Dina, A. F. Ghaleb. Effect of a harmonic surface pressure on wave propagation over a beach. Scientific Reports, 2024, 14(1) doi:10.1038/s41598-024-67443-6 | |
| 5. | Zegao Yin, Guilin Yang, Yanxu Wang, et al. Numerical simulations of breaking wave propagation through the vegetation on a slope based on a drag coefficient prediction model. Ocean Engineering, 2024, 291: 116440. doi:10.1016/j.oceaneng.2023.116440 | |
| 6. | Yanxu Wang, Yong Liu, Zegao Yin, et al. Numerical simulation of wave propagation through rigid vegetation and a predictive model of drag coefficient using an artificial neural network. Ocean Engineering, 2023, 281: 114792. doi:10.1016/j.oceaneng.2023.114792 | |
| 7. | Nanda Shabrina, Defri Ahmad. Analisis Jalur Terdekat Menuju Bangunan Shelter Evakuasi Tsunami di Kota Padang Menggunakan Network Analyst. Jurnal Pendidikan Matematika, 2023, 1(2): 13. doi:10.47134/ppm.v1i2.202 | |
| 8. | Jingming Hou, Wei Lu, Tingting Fan, et al. Tsunami hazard and mitigation analysis for bathing beaches in China based on numerical simulations. Acta Oceanologica Sinica, 2022, 41(12): 27. doi:10.1007/s13131-022-2027-z | |
| 9. | Shuangjin Leng, Guoji Xu, Qinghong Wu, et al. Review on tsunami–bridge interaction. Intelligent Transportation Infrastructure, 2022, 1 doi:10.1093/iti/liac021 | |
| 10. | J. X. Huang, K. Qu, X. H. Li, et al. Performance Evaluation of Seawalls in Mitigating a Real-World Tsunami Wave Using a Nonhydrostatic Numerical Wave Model. Journal of Marine Science and Engineering, 2022, 10(6): 796. doi:10.3390/jmse10060796 | |
| 11. | Ke Qu, Yancheng Lie, Xu Wang, et al. Numerical Analysis on Influences of Emergent Vegetation Patch on Runup Processes of Focused Wave Groups. Journal of Marine Science and Engineering, 2022, 11(1): 8. doi:10.3390/jmse11010008 | |
| 12. | Rui-dong An, Da-peng Jiang, Ching-hao Yu, et al. Numerical Simulation of Tsunami-Like Wave Impacting on Breakwater by CLSVOF/IB Method. China Ocean Engineering, 2021, 35(5): 676. doi:10.1007/s13344-021-0059-3 | |
| 13. | K. Qu, G. Y. Lan, S. Kraatz, et al. Numerical Study on Wave Attenuation of Tsunami-Like Wave by Emergent Rigid Vegetation. Journal of Earthquake and Tsunami, 2021, 15(06) doi:10.1142/S1793431121500287 |
