Intraseasonal variability of the surface zonal current in the equatorial Indian Ocean: Seasonal differences and causes

1. Introduction

The Indian Ocean contributes to the global material and energy balance (Reppin et al., 1999; Schott and McCreary, 2001; Chen et al., 2021). The equatorial currents in the Indian Ocean are the important part of the global circulation system. Observations and numerical simulations suggest that zonal currents in the equatorial Indian Ocean show substantial intraseasonal variability (ISV) (Farrar and Weller, 2006; Kessler et al., 1995; Masumoto et al., 2005; Chen et al., 2019), which plays a vital role in the transportation of heat and volume in the Indian Ocean, and affects regional and global climate change (Schott et al., 2009). The surface zonal currents in the equatorial Indian Ocean flow eastward during boreal spring and fall and are forced by the equatorial westerlies (Wyrtki, 1973), but weaken and even reverse direction in summer and winter (Joseph et al., 2012). The direction of the surface circulation changes seasonally, and the seasonal variation is coincident with the atmospheric forcing (Xuan et al., 2014). These studies imply that there may be an important seasonal difference in current intraseasonal variability (ISV) in the equatorial Indian Ocean.

In the eastern basin, the current ISV is substantial at 80°–90°E, especially for the equatorial upper ocean currents. Mooring observations have revealed that the ISV of currents at 90°E has a dominant period of 30–50 d and can extend to 390 m depth, but most of the energy is confined to the upper 100 m of the ocean (Masumoto et al., 2005). Kindle and Thompson (1989) reproduced the observed 40–60-day oscillations (Luyten and Roemmich, 1982) and 26–50-day oscillations (Mysak and Mertz, 1984; Schott et al., 1988) in the western basin using a reduced gravity model. Previous studies have well reported the significance of the current ISV in the Indian Ocean, however less attention is paid to the seasonal difference.

As for the driving force of the intraseasonal zonal current, a number of studies found that there are mainly two kinds. The intraseasonal zonal currents in the eastern basin can be driven effectively by the atmospheric intraseasonal oscillations (ISOs). Currents with a period of 30–50 d (Masumoto et al., 2005) and 60 d (Han et al., 2004) are directly driven by the zonal winds between 80°E and 90°E. Currents with a period of 90 d result from wind stress and are strengthened by the basin resonance of the equatorial wave-guide (Han et al., 2001, 2004). The equatorial waves process also occur in the generation of intraseasonal zonal currents. The atmospheric ISO induces the intraseasonal sea-level anomaly (SLA) around the Equator, which propagates eastward across a broad range of phase speeds for the low baroclinic Kelvin waves (Iskandar and McPhaden, 2011). The oceanic internal instabilities also play an important role. Kindle and Thompson (1989) and Schott et al. (1988) found that barotropic instability is the mechanism that generates the 50-day oscillations from the results of a numerical shallow-water model. Sengupta et al. (2001) concluded that the oceanic internal instabilities of the background current produce the surface zonal current ISV (u ISV) in the western basin and south of Sri Lanka by conducting numerical experiments on the seasonal wind field. Brandt et al. (2003) pointed out that the u ISV in the western Indian Ocean is related to the oceanic internal instabilities of the Somali current when it crosses the equator. Although the atmospheric ISOs (e.g., Brandt et al., 2003; Han et al., 2001; Han, 2005; Iskandar and McPhaden, 2011) and oceanic internal instabilities (e.g., Reppin et al., 1999; Sengupta et al., 2001), as elaborated above, are considered to modulate the u ISV, the previous studies have not clearly quantified the respective contribution of the two driving forces in the generation of u ISV.

An important characteristic of the atmospheric ISOs in the Indian Ocean is that their existence, structure, evolution, and propagation are different in boreal summer (May to October) and boreal winter (November to April). The substantial atmospheric ISOs in the tropical Indian Ocean have an annual cycle, which can be represented by the Madden–Julian Oscillation (MJO; e.g., Madden and Julian, 1971; Hendon et al., 1998; Adames and Kim, 2015) and the Indian summer monsoon ISO (MISO; e.g., Zhu and Wang, 1993; Lawrence and Webster, 2002; Suhas et al., 2013). The MJO and the MISO are vigorous during boreal winter and boreal summer, respectively (Hazra and Krishnamurthy, 2018). In general, the atmospheric ISOs associated with the MJO propagating eastward along the equator. The atmospheric ISOs associated with the MISO pass northward from the equatorial Indian Ocean to the Indian subcontinent together with weak eastward propagation along the equator (Jiang et al., 2004). Both the MJO (e.g., Kemball-Cook and Wang, 2001; Zhou and Murtugudde, 2010; Duan et al., 2019) and the MISO (e.g., Sikka and Gadgil, 1980; Yasunari, 1980) can cause strong air-sea interaction, also impact the cloudiness above the Indian Ocean. Han et al. (2001) used nonlinear and linear 4.5-layer ocean models and confirmed the intraseasonal zonal current that is excited by intraseasonal winds associated with the MJO. Senan et al. (2003) used an ocean general circulation model to show that the westerly wind burst related to the MISO can drive strong equatorial eastward jets with intraseasonal fluctuations. Chen et al. (2017) suggested that both the MJO and the MISO are potential candidates to produce the strong intraseasonal variability in the meridional current at 5°N. Overall, as the wind-stress anomalies related to the MJO are different from those related to the MISO (Kikuchi and Wang, 2010), given the reverse direction of background currents during boreal summer and boreal winter, the relationship between the u ISV in the equatorial Indian Ocean and the MJO/MISO remains an interesting topic which is short of deep investigation in previous studies.

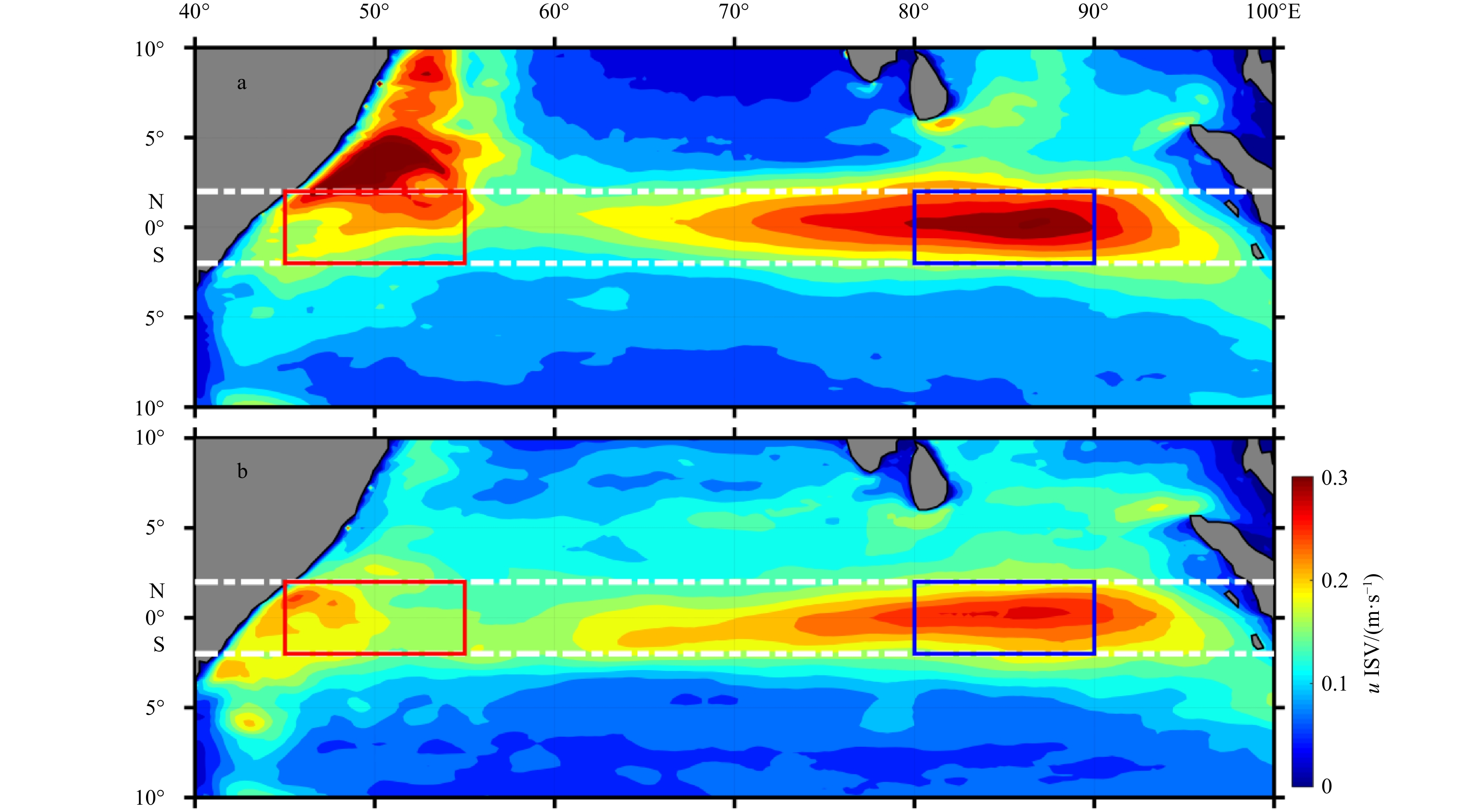
As shown in Fig. 1 (data validation can be found in Section 3.1), the strength and spatial distribution of the u ISV in boreal summer (May–October) are considerably different from that in boreal winter (November–April). May and November are transitional months. The seasonal difference between boreal summer and boreal winter is still considerable when these two months are excluded. Although many studies have examined the u ISV, the seasonal differences in the u ISV and the underlying processes remain unknown, as well as the possibility of different effects of the MJO and the MISO on the generation of the u ISV. The above unknowns will be explicitly investigated by this study.

Figure  1.  Maps of the u ISV (30–105 d) averaged over 5–50 m from MR in boreal summer (May–October, a) and boreal winter (November–April, b). The blue and red boxes show the regions for quantifying the u ISV in the eastern and western basins, respectively. The white dashed lines mark the equatorial region (2°S–2°N).

DownLoad: Full-Size Img PowerPoint

By analyzing in situ observations and conducting ocean circulation model experiments, this study examines the u ISV in the equatorial Indian Ocean, quantifies the contributions of the atmospheric ISOs and the oceanic internal instabilities, and investigates the seasonal difference and the different impacts of the MJO and MISO on the u ISV. The remainder of the paper is organized as follows. Section 2 describes the data and the ocean models used for the analysis. Section 3 presents the observed and modeled features of the u ISV, and the seasonal differences of the u ISV and the driving processes are given inside as well. Section 4 summarizes the primary findings of this study.

2. Data and ocean models

2.1 Data

The current measurements from two equatorial moorings of the Research Moored Array for African-Asian-Australian Monsoon Analysis and Prediction (RAMA; McPhaden et al., 2009) program are used to examine the u ISV and to validate the Hybrid Coordinate Ocean Model (HYCOM) simulation performance. One mooring deployed at 0°, 80.5°E provides data at 25–350 m with a 5 m vertical resolution from 27 October 2004. The other mooring deployed at 0°, 90°E provides data at 40–410 m with a 10 m vertical resolution from 14 November 2000. The daily zonal current data from October 2004 to August 2012 at 0°, 80.5°E and from January 2001 to December 2012 at 0°, 90°E are used in our analysis.

The 0.25°×0.25°, daily Cross-Calibrated Multi-Platform (CCMP) version 2.0 satellite ocean surface wind vectors (Atlas et al., 2008) during 2001–2012 are analyzed to understand the relationship between the u ISV and wind stress associated with the atmospheric ISOs. A drag coefficient of 1.43×10⁻³ and an air density of 1.225 kg/m³ are used to calculated the wind stress (Weisberg and Wang, 1997). The satellite-observed 1°×1° daily outgoing longwave radiation (OLR) data (Liebmann and Smith, 1996) are also analyzed to understand the causes of the seasonal differences of the u ISV between May–October and November–April.

2.2 OLR-related MJO index

The substantial tropical ISOs show two distinct patterns in boreal summer and boreal winter. The variability center propagates eastward along the equator in boreal summer, and northward from the equatorial region into off-equatorial monsoon trough regions. The boreal summer and boreal winter patterns are accurately represented by a bimodal index (Kikuchi and Wang, 2010; Kikuchi et al., 2012), which consists of the MJO and the boreal summer intraseasonal oscillation (BSISO, or MISO; May–October).

Several indexes are developed to track the movement of these tropical intraseasonal oscillations, such as the all-season real-time multivariate MJO index (RMM index; Wheeler and Hendon, 2004), the bimodal index (Kikuchi et al., 2012), and the OLR-related MJO index (OMI; Kiladis et al., 2014).

In many previous studies, the MJO is identified by the RMM index in the WH04 (Wheeler and Hendon, 2004). Indeed, the eastward-propagating atmospheric ISO (MJO) is well represented by the WH04 (e.g.,Dasgupta et al., 2020; Jin et al., 2012). However, WH04 is unsatisfactory in modulating the northward-propagating atmospheric ISO (MISO) in May–October (Dey et al., 2019). In comparison, the substantial atmospheric ISOs identified by the bimodal index are more standardized than the WH04. Furthermore, the bimodal index provides more detailed information on the predominant ISO mode at a particular time (Kikuchi et al., 2012). Besides the bimodal index, the OMI is another better index for capturing the northward-propagation characteristics of the MISO in boreal summer. The OMI capabilities in monitoring and predicting the MISO are examined by Wang et al. (2018). They found the OMI has a high correlation with the bimodal index, and suggest that the OMI does the best representation of both northward and eastward propagation of intraseasonal convection in summer than the RMM index and the bimodal index. Given that our study focuses on the seasonal difference in the u ISV, we use the OMI to identify the substantial atmospheric ISOs associated with the MJO/MISO, to investigate the relationship between the MJO/MISO and the seasonal difference in the u ISV.

2.3 HYCOM and experiments

The Hybrid Coordinate Ocean Model (HYCOM; e.g.,Chassignet et al., 2006) is used in this study to characterize the intraseasonal features of the equatorial currents and to explore the dynamical process in the Indian Ocean. The model has a horizontal resolution of 0.25°×0.25° and 26 vertical layers in the Indian Ocean Basin (50°S–30°N, 30°–122.5°E). The model is spun up for 30 years using monthly climatological forcing to reach a steady state, and then is integrated forward by 0.25°×0.25° cross-calibrated Multi-Platform (CCMP) satellite ocean surface winds (Atlas et al., 2008) from 1 March 2000 to 31 December 2010 and by the daily 0.25°×0.25° gridded Advanced Scatterometer (ASCAT) satellite ocean surface winds (Bentamy and Fillon, 2012) from 1 January 2011 to 31 December 2012. Details of the model configuration and the surface atmospheric forcing fields can be found in Li et al. (2014). This experiment is named the main run (MR).

We performed two additional experiments as well as the MR, named NoISO and NoSTRESS (Table 1). In the case of NoISO, the atmospheric forcing fields are fully filtered with a 105-day low-pass Lanczos digital filter. The difference between MR and NoISO (MR-NoISO) measures the forcing effects of the atmospheric ISOs on the ocean, whereas NoISO measures the contribution from oceanic internal instabilities. In NoSTRESS, however, only the wind stress is 105-day low-pass filtered. The difference between MR and NoSTRESS (MR-NoSTRESS) thus quantifies the effects of the intraseasonal wind stress on the ocean. The outputs of the three experiments are stored as 3-day mean data, and the records of 2001–2012 are used in our analysis. Unless otherwise specified, surface currents from HYCOM are examined for the upper 50 m. To investigate the intraseasonal variabilities of the surface zonal currents, velocity, wind-stress anomalies, and OLR, we show the 30–105-day-filtered intraseasonal components.

Table  1.  Summary of HYCOM experiments

Experiment	Description
MR	complete run
NoISO	remove all ISO effects
NoSTRESS	remove ISO wind stress
MR-NoISO	estimated ISO effects
MR-NoSTRESS	estimated wind stress ISO effects
Note: ISO signals in forcing fields are removed with a 105-day low-pass Lanczos filter.

 | Show Table

DownLoad: CSV

3. Results

3.1 Model/data comparison

The HYCOM model performance in simulating the u ISV is verified by comparing it with RAMA observations. The amplitude and phases of the observed and simulated ISV of the equatorial current agree well with each other (Fig. 2). The correlation coefficient (R) between RAMA and HYCOM reach 0.82 at 80.5°E and 0.79 at 90°E, respectively. The standard deviations (STDs) of the intraseasonal zonal currents in the upper 40–70 m from RAMA and the upper 50 m from HYCOM are 0.21 m/s and 0.27 m/s at 0°, 80.5°E, and 0.22 m/s and 0.28 m/s at 0°, 90°E, respectively. NoISO successfully simulates the low-frequency u (compare Figs S1b and c in Supplementary information) and thus the NoISO is suitable for examining the contribution of the oceanic internal instabilities to the u ISV.

Figure  2.  Intraseasonal (30–105-day) zonal current averaged over the upper 70 m from the RAMA mooring (red lines) and the upper 50 m from MR (black lines) at 0°, 80.5°E (a) or at 0°, 90°E (b) in 2005–2011. The shadow in the background refers to boreal summer (May to October).

DownLoad: Full-Size Img PowerPoint

Earlier studies have also found that HYCOM well simulates the fundamental oceanic characteristics in the Indian Ocean, including variations of sea surface temperature (Li et al., 2013, 2014), sea surface salinity (Li et al., 2015, 2017), sea surface height (Chen et al., 2017), and the equatorial undercurrent (Chen et al., 2019). We thus use HYCOM outputs together with RAMA observations to explore the seasonal and special differences of the intraseasonal equatorial current and the physical processes underlying.

3.2 Spatial distribution and the dominant factors

To understand the spatial distribution of the u ISV, Fig. 3a shows the STD of intraseasonal zonal currents averaged over 5–50 m, 2°N–2°S from HYCOM MR during 2001–2012. There are two extrema along the equator (black line in Fig. 3a). A peak with large amplitude occurs in the eastern basin, especially at around 87°E with an amplitude of 0.26 m/s. Compared with the eastern basin, the amplitude of u ISV in the western basin is evidently weaker. However, a peak is still seen at around 47°E with an amplitude of 0.20 m/s.

Figure  3.  The standard deviations of the u ISV (m/s) from HYCOM experiments and the intraseasonal wind stress (N/m²) from CCMP along the equator (40°E to 100°E) during 2001–2012. The u ISV is averaged over 5–50 m, 2°S–2°N from MR (black line), MR-NoISO (yellow line; atmospheric ISOs), NoISO (red line; oceanic internal instabilities) and MR-NoSTRESS (orange line; intraseasonal wind stress). The Intraseasonal zonal wind stress are shown by blue-dashed lines, and labeled on the right axis. Therein, a, b and c are for all-season, the boreal summer (May to October) and the boreal winter (November to April), respectively. Note that the thin black, yellow and red lines in each panel represent the mean value of the u ISV from MR, MR-NoISO, and NoISO, respectively.

DownLoad: Full-Size Img PowerPoint

The results from NoISO and NoSTRESS are analyzed to understand the generation of the u ISV. Oceanic internal instabilities, measured by NoISO, contribute substantially to the u ISV in the western basin near 47°E (red line in Fig. 3a). MR-NoISO, which measures the forcing effect of atmospheric ISOs on the ocean (yellow line in Fig. 3a), agrees well with the MR, implying that the atmospheric ISOs play an important role in the u ISV of the whole equatorial region rather than only in the eastern basin. The results from MR-NoSTRESS are consistent with that from MR-NoISO and suggest that the contribution of atmospheric ISOs to the ISV is mainly through intraseasonal wind-stress forcing. The stronger intraseasonal wind-stress anomalies appear in the eastern basin (blue dashed line in Fig. 3a).

To further quantify the contribution of atmospheric ISOs and oceanic internal instabilities, the u ISV averaged over 2°S–2°N, 80°–90°E (blue box in Fig. 1) and 2°S–2°N, 45°–55°E (red box in Fig. 1) from 5 m to 50 m are chosen to investigate the u ISV in the eastern and western basins, respectively. Owing to the similar features of atmospheric ISO and oceanic internal instabilities contributions to the u ISV from 2001 to 2012, we only show the results for 2005–2011 here to clearly compare the time series from the MR, MR-NoISO, and NoISO (Fig. 4).

Figure  4.  Time series of the u ISV (m/s) from the MR (black line), MR-NoISO (red line), and NoISO (blue line), averaged over 5–50 m, 2°S–2°N, 80°–90°E (a, the east box in Fig. 1), and 5–50 m, 2°S–2°N, 45°–55°E (b, the west box in Fig. 1). Gray shading indicates boreal summer (May to October). Owing to the similar features in 2001–2012, we show only the results in 2005–2011.

DownLoad: Full-Size Img PowerPoint

In the eastern basin, the STDs of the u ISV are 0.22 m/s for HYCOM MR, 0.20 m/s for MR-NoISO, and 0.07 m/s for NoISO during 2001–2012 (Fig. 4a). With oceanic internal instabilities forcing, the STD_(NoISO)/STD_(MR) of the intraseasonal zonal currents is 32%, and with atmospheric ISO forcing, the STD_(MR-NoISO)/STD_(MR) is 91%. It should be mentioned that the contributions of the atmospheric ISOs and oceanic internal instabilities do not add up linearly to 1 due to the nonlinearity of the STD calculation formula. The correlation coefficient between MR and MR-NoISO (NoISO) is 0.94 (0.44). In addition, it is clear that the u ISV in the MR-NoSTRESS is close to the u ISV in the MR-NoISO (compare the orange and yellow lines in Fig. 3a). This means that the atmospheric ISOs, through intraseasonal wind stress, dominate the u ISV in the eastern basin, as suggested by previous studies (Han, 2005; Masumoto et al., 2005; Nagura and McPhaden, 2012).

In the western basin, both the atmospheric ISOs and the oceanic internal variabilities contribute to the u ISV (Fig. 4b). The correlation coefficient between MR and NoISO (MR-NoISO) is 0.50 (0.70), and the STDs from MR and NoISO (MR-NoISO) are 0.11 m/s and 0.08 m/s (0.09 m/s). Previous studies have suggested that the intraseasonal zonal current in the western basin is caused by oceanic internal instabilities (Schott et al., 2009; Sengupta et al., 2001), specifically from gyres in the Somali current (Brandt et al., 2003). Herein, our results reveal that even in the western basin, the atmospheric ISOs have a slightly larger contribution to the u ISV. Further detail about the influence of the atmospheric ISOs on the u ISV in the western basin is given in Section 3.4.

3.3 Seasonal differences in the eastern basin

Figure 1 shows the obvious seasonal difference in the u ISV at the Equator. In Sections 3.3 and 3.4, by combining observations and model outputs, we further examine the seasonal difference of the u ISV and the related dynamics in the eastern and western basins, respectively.

3.3.1 Seasonal differences

The composite analysis based on RAMA observations at 80.5°E and 90°E reveals the substantial seasonal difference in the u ISV in the eastern basin (Fig. 5). The +1 STD of the intraseasonal zonal current velocities is used to identify positive strong ISV events. On the basis of this criterion, we identify 46 and 53 (28 and 33) positive ISV events during May–October and November–April at the 80.5°E (90°E) site, respectively. The days with a maximum value are taken as Day 0 in the composite analysis result (t=0 in Fig. 5). Then, the ISV composites from RAMA for 40 d before (−40 d) and 40 d after (+40 d) Day 0 are obtained. The composite current ISV amplitude reaches 0.29 m/s in May–October versus 0.18 m/s in November to April at 0°, 80.5°E and 0.28 m/s versus 0.18 m/s at 0°, 90°E. The composite analysis of the mooring sites suggests that the u ISV in boreal summer (May to October) is about 1.5 times larger than that in boreal winter (November to April).

Figure  5.  Composite analysis of the u ISV during May–October (red line) and November–April (blue line) from the RAMA observations at the 0°, 80.5°E (a) and 0°, 90°E (b) moorings.

DownLoad: Full-Size Img PowerPoint

On the basis of the interesting phenomenon found by analyzing the observations, we further investigate the seasonal difference along the equator using the simulations. The HYCOM results verify that the stronger u ISV in the eastern basin is a typical feature. On the basis of the u ISV averaged over 2°S–2°N, 80°–90°E from HYCOM MR during 2001–2012, 33 and 32 strong events are identified in boreal summer (May to October) and boreal winter (November to April), respectively. Specifically, the amplitude of the strong u ISV events is 0.40 m/s in boreal summer (May to October) compared with 0.32 m/s in boreal winter (November to April). The amplitude is much stronger and the ranges are wider in boreal summer (May to October). As revealed by the observations and the simulations, the seasonal difference of the u ISV is evident in the eastern basin. Comparing the u ISV from the HYCOM MR and other experiments helps to determine the cause of the seasonal difference. As the STD of the u ISV in NoISO presents a weak seasonal difference in the eastern basin (compare red lines in Figs 3b and c), and the amplitude and the ranges of the strong events in MR-NoISO are stronger and wider in boreal summer (Fig. 6b). Comparing the strong events of the MR (Fig. 6a) with the MR-NoISO, we can find that the distribution of the u ISV is similar. In conclusion, the atmospheric ISOs, and specifically the intraseasonal wind stress, dominate the seasonal difference in the u ISV in the eastern basin.

Figure  6.  The strong u ISV events averaged over 5–50 m in the eastern or western box. a and b. Composed based on the strong u ISV events at 2°S–2°N, 80°–90°E (the east box in Fig. 1) from MR in boreal summer (left panel) and boreal winter (right panel). c and d. Similar but composed based on the strong u ISV events at 2°S–2°N, 45°–55°E (the west box in Fig. 1) and from MR-NoISO (c) and NoISO (d).

DownLoad: Full-Size Img PowerPoint

Determining how the dynamic process occurs is important to understanding the connection between wind stress and the u ISV. We perform lagged correlation analysis between the u ISV averaged over 2°S–2°N, 80°–90°E and wind stress at each grid point in boreal summer (May to October) and boreal winter (November to April), respectively (Fig. 7). From the correlation analysis, we find an area of positive correlation over the equatorial region 60°–100°E with a correlation coefficient larger than 0.5. Then we composite wind stress based on the strong u ISV events in the eastern basin. The composite analysis reveals that strong westerlies also occupy this region (white lines in Fig. 7) when wind stress leads by 10–0 d in boreal summer and boreal winter. The correlation region of the composite westerlies in the boreal summer looks different to that in boreal winter and the amplitude is stronger. The u ISV in the equatorial Indian Ocean is directly forced by wind in boreal summer and boreal winter. In the wind-driven process, two types of waves that respond to the wind stress are equatorial trapped Kelvin waves and long equatorial Rossby waves. The intraseasonal equatorial zonal wind forcing generates the u ISV by the directly forced Kelvin and Rossby waves (e.g., Shinoda et al., 2008; Iskandar, 2011). The equatorial Kelvin waves propagate eastward along the equator. The Rossby waves propagate off the equator with a westward group velocity for long waves and an eastward group velocity for short waves. In comparison, it takes 20–30 d to set up the equatorial undercurrent in the eastern basin, which is mainly caused by the reflected Rossby waves associated with the intraseasonal equatorial zonal wind forcing (Chen et al., 2019).

Figure  7.  Correlation coefficient (with a 95% significance level; color shading) between intraseasonal zonal wind stress (τ_x) and the u ISV averaged over 2°S–2°N, 80°–90°E (the east box in Fig. 1) from MR-NoISO in boreal summer (May to October; left panel) and in boreal winter (November to April; right panel) when τ_x leads by 10 d, 5 d, 0 d, −5 d, and −10 d. The white contours represent the coefficient value of 0.35. Based on the eastern strong u ISV events from MR, the vectors are the intraseasonal wind stress before or after the eastern strong u ISV events (t=0).

DownLoad: Full-Size Img PowerPoint

3.3.2 Relationship with the MISO and MJO

The main atmospheric ISOs in the Indian Ocean are those related to the MJO, the intensity of which is stronger in winter, and to the MISO, the influence of which is more substantial in summer (Kikuchi et al., 2012). As the wind anomalies of the MJO differ in their temporal–spatial features from that of the MISO, these two important intraseasonal atmospheric oscillations are expected to induce varied intraseasonal zonal currents in the equatorial Indian Ocean. From the correlation analysis for May–October, the positive correlation region propagates from the equator to 10°N from Day 0 to Day 10 (t=10, t=5 in Fig. 7a) after the strong u ISV events occur (t=0), but for November–April, the positive correlation region propagates eastward symmetrically about the Equator (t=10, t=5 in Fig. 7b). It is possible that the seasonal difference between the MJO and MISO, have different influences on the u ISV generation. We thus further investigate the relationship between the seasonal difference of the u ISV with the MISO and MJO by investigating the propagation of the MISO and MJO, and the related wind stress.

On the basis of the seasonal differences, we divide the OMI index into the May–October index for the MISO and the November–April index for the MJO. Based on the index from 2001 to 2012, we identify substantial MISO and MJO events, with an index amplitude larger than +1 STD, and then obtain the composite intraseasonal OLR and wind-stress anomalies for the first four phases of the MISO (left panel in Fig. 8) and MJO (right panel in Fig. 8) .

Figure  8.  Composite intraseasonal (30–105-day filtered) OLR (W/m²; color) and the intraseasonal wind stress (N/m² ; white vector) under Phases 1–4 of the MISO index (left panel) and the MJO index (right panel) that based on the OMI.

DownLoad: Full-Size Img PowerPoint

It can be clearly seen that in boreal summer (May to October), the atmospheric ISOs associated with the MISO propagate northward from the equator to the higher latitudes in the tropical Indian Ocean. In addition, the negative OLR is located northeastward like the positive correlation region in May–October (t=10, t=5 in Fig. 7a). In comparison, in boreal winter (November to April), the atmospheric ISOs associated with the MJO propagate eastward along the equator symmetrically like the positive correlation region in November–April (t=10, t=5 in Fig. 7b). Moreover, the composite wind stress shows the seasonal difference. The amplitude of the intraseasonal zonal wind stress over the near-equatorial region (marked by the white contours in the subplot -10 d of Fig. 7) at Phases 1–4 of the MISO are 3.98×10⁻² N/m², 5.97×10⁻² N/m², 6.38×10⁻² N/m² and 5.17×10⁻² N/m², respectively, while the amplitude at Phases 1–4 of the MJO are 1.31×10⁻² N/m², 3.07×10⁻² N/m², 5.30×10⁻² N/m² and 5.01×10⁻² N/m², respectively. The intraseasonal OLR and the wind stress anomalies are strongest under Phase 3 of the MISO/MJO. The wind stress related to the MISO is stronger than to the MJO Phase 3. Choosing one standard both for the MISO/MJO and u ISV composition analysis is helpful to figure out the different influences between the MISO and MJO on the u ISV. Thus, based on the OMI, we composite the u ISV onto the phases of the MJO/MISO (Fig. 9). The positive u ISV is strongest under Phase 3 of the MISO/MJO accordingly. Impacted by the MISO Phases 2–3, the u ISV is stronger than that impacted by the MJO Phases 2–3. These results suggest that, the larger u ISV in boreal summer is attributed to the stronger wind stress anomalies associated with the MISO.

Figure  9.  Composite intraseasonal (30–105-day filtered) zonal currents (m/s) under Phases 1–8 of the MISO index (left panel) and the MJO index (right panel) that based on the OMI. The 10 d and 5 d means the days after the MISO/MJO happened.

DownLoad: Full-Size Img PowerPoint

3.4 Seasonal differences in the western basin

As both the intraseasonal wind stress and the oceanic internal instabilities contribute to the u ISV in the western basin (Figs 3a and 4b), we conduct composite analysis from MR-NoISO and NoISO (Figs 6c and d) to understand the causes of the seasonal difference of the u ISV averaged in 2°S–2°N, 45°–55°E.

Driven by the atmospheric ISOs, the averaged u ISV in MR-NoISO is 0.11 m/s and 0.09 m/s in boreal summer (May to October) and boreal winter (November to April), respectively. The strong u ISV events (Fig. 6c) reach 0.19 m/s in boreal summer larger versus 0.15 m/s in boreal winter, based on 29 events in boreal summer (May to October) and 28 events in boreal winter (November to April). The lagged correlation between intraseasonal zonal wind stress and the u ISV suggests that the nearshore wind stress to the west of 60°E contributes to the western u ISV (Supplementary Fig. S2). It takes 0–5 days for the local wind stress to induce the ISV.

Associated with the oceanic internal instabilities, the averaged u ISV in NoISO is 0.09 m/s and 0.06 m/s in boreal summer (May to October) and boreal winter (November to April), respectively. The strong u ISV events (Fig. 6d) have a larger amplitude of 0.14 m/s in boreal summer (May to October) than 0.10 m/s in boreal winter (November to April), based on 18 events in boreal summer and 23 events in boreal winter. Without the external forcing, the currents ISV can be raised from the background circulations instability (Wang et al., 2016). By the oceanic internal instabilities, the energy can converted from mean flow to the intraseasonal currents. Next, we discuss the connection between ISV energy and the mean flow energy which is quantified by the baroclinic (T2) and barotropic conversion (T4). The T2 and T4 can be calculated via the energy budget analysis (Appendix; Chen et al., 2017), and be averaged at 2°S–2°N, 45°–55°E to obtain regional means (the right panel of Fig. 10). Additionally, the energy budget is calculated for the upper 50 m from the MR simulation currents. Because the baroclinic conversion (T2, 10⁻⁹ m⁻²·s⁻³) is much less than the barotropic conversion (T4, 10⁻⁷ m⁻²·s⁻³) in the upper mixed layer, which means the potential energy conversion is small, thus the influence of the T2 is negligible in our analysis. Then the energy budget could be simplified as kinetic-energy budget. The values of M-KE over the region of the western basin are depicted in the left panel of Fig. 10.

Figure  10.  The background current (m/s; vector) averaged at 5–50 m and meanflow kinetic energy (M-KE; m²/s²; color) in boreal summer (May to October, a) and in boreal winter (November to April, b) from MR; and the daily averaged barotropic conversion (T4; m²/s³) at 2°S–2°N, 45°–55°E (the west box in Fig. 1) during 2001–2012 (c). The zonal component and the meridional component of T4 are shown as red and gray solid lines in c.

DownLoad: Full-Size Img PowerPoint

The background current, its kinetic energy (M-KE) and the T4 show substantial seasonal differences in the western Indian Ocean (Fig. 10). Stronger mean flow and the M-KE occur in boreal summer (May to October). A strong gyre called the “Southern Gyre” occupies the western Indian Ocean in boreal summer (May to October), but it disappears in boreal winter (Swallow and Fieux, 1982). T4 is largely positive in boreal summer (May to October). Positive T4 indicates that, the energy is converted from the M-KE to the intraseasonal kinetic energy (ISV-KE; Zhang et al., 2020; Oey et al., 2008; Chen et al., 2015). Energy budget analysis reveals that, in boreal summer (May to October), stronger mean flow converts more kinetic energy to the intraseasonal currents by the barotropic conversion (T4). Further, the T4 can be decomposed into horizontal shear of zonal currents item (red line) and horizontal shear of meridional flows item (gray solid line). Compared with the black line (the right panel of Fig. 10), the total barotropic conversion is mainly determined by the horizontal shear of zonal currents item, which indicates that the ISV energy is mainly supplied by the horizontal shear of zonal currents item.

Combining the forcing of the local wind stress and the barotropic conversion of mean flow, in the western basin, the larger u ISV occurs in boreal summer (May to October). In MR, the u ISV is 0.11 m/s and 0.10 m/s in boreal summer (May to October) and boreal winter (November to April), and the strong u ISV events reach 0.20 m/s and 0.18 m/s in boreal summer (May to October) and boreal winter (November to April).

4. Summary and discussion

Intraseasonal variability is intense in the equatorial Indian Ocean, and the resulting potential for the air-sea coupled interaction is important in the Indian Ocean climate. By combining the RAMA data and a series of HYCOM numerical experiments, we found two centers of u ISV in the equatorial Indian Ocean: 80°–90°E in the eastern basin and 45°–55°E in the western basin (Fig. 3). We then quantified the driving forces. The results from the correlation analysis and composite analysis reveal that the two u ISV centers have obvious seasonal differences (Fig. 1). In the eastern basin, the u ISV is mainly due to atmospheric ISOs (Fig. 4a), as the u ISV driven by atmospheric ISOs (MR-NoISO) reaches 91% of the u ISV in MR. RAMA observations suggest that the strong u ISV events in boreal summer (May to October) are about 1.5 times larger than in boreal winter (November to April) (Fig. 5), and the HYCOM simulations confirm the seasonal difference along the Equator (Figs 3b and c). The seasonal difference in the eastern basin is predominantly caused by the atmospheric ISOs (Figs 6a and b), specifically, the local wind stress through directly forced Kelvin and Rossby waves (Fig. 7). Interestingly, the MJO and the MISO have a different effect on the generation of u ISV in the eastern basin. By calculating the zonal wind stress in the correlation region (r>0.35 in Fig. 6), the maximum amplitude is 6.38×10⁻² N/m² and 5.30×10⁻² N/m², which is associated with Phase 3 of the MISO and Phase 3 of the MJO, respectively (Fig. 8). The stronger wind stress is associated with the MISO in boreal summer (May to October), which induces stronger u ISV (Fig. 9).

In the western basin, in addition to the oceanic internal instabilities suggested by previous studies, atmospheric ISOs are verified to contribute substantially to the u ISV. It takes 0–5 d for nearshore wind stress to generate the u ISV. The strong u ISV event forced by atmospheric ISOs (MR-NoISO) is 0.19 m/s in boreal summer compared with 0.15 m/s in boreal winter (Fig. 6c). The strong u ISV event associated with oceanic internal instabilities (NoISO) shows seasonal differences as well (Figs 3a and b), with an amplitude of 0.14 m/s in boreal summer versus 0.10 m/s in boreal winter (Fig. 6d). Kinetic energy budget analysis suggests that the energy of the background current shows substantial seasonal differences and converts more energy to the intraseasonal currents in boreal summer by barotropic conversion (Fig. 10). As a result, the western u ISV is stronger in boreal summer. Resulted from the local intraseasonal winds and the barotropic conversion, the strong u ISV events in MR reach an amplitude of 0.20 m/s in boreal summer versus 0.18 m/s in boreal winter.

The intraseasonal winds are active along the equator during Indian Ocean Dipole (IOD) events (Shinoda and Han, 2005), suggesting that the IOD may modulate the interannual differences of the u ISV. An extreme ENSO event can disrupt the circulation balance of the Indo-Pacific Ocean, causing an exceptionally weak ISV in the southeastern Indian Ocean through suppressing the South Equatorial Current instabilities (Lau and Waliser, 2012; Chen et al., 2020). Large-scale variability effectively modulates the intraseasonal variation of the current in the Indian Ocean. The energy exchange between the large-scale variability in the atmosphere and the ISV in the ocean is necessary for improving an understanding of the Indian Ocean. A quantitative examination of the large-scale variability modulating the equatorial currents ISV is an interesting theme for future studies. It is hoped that our study would be valuable in expanding the knowledge of the ISV of currents, and stressing the importance of the seasonal differences in the atmospheric ISOs in the Indian Ocean.

Acknowledgements

The RAMA data was obtained at https://www.pmel.noaa. gov/gtmba/pmel-theme/indian-ocean-rama. The CCMP data are available online at http://data.remss.com/ccmp/v02.0/, and the details are retrieved from https://climatedataguide.ucar.edu/climate-data/ccmp-cross-calibrated-multi-platform-wind-vector-analysis. The OLR data and detailed description are at http://www.esrl.noaa.gov/psd/data/gridded/data.olrcdr.interp.html. The OMI index and the EOFs at https://psl.noaa.gov/mjo/mjoindex. The bimodal index and the details are from http://iprc.soest.hawaii.edu/users/ kazuyosh /Bimodal_ISO.html. This study is supported by the China-Sri Lanka Joint Center for Education and Research in the Chinese Academy of Sciences. The numerical simulation is supported by the High Performance Computing Division in the South China Sea Institute of Oceanology.