Experimental study of freak waves due to three-dimensional island terrain in random wave
-
Abstract: An experimental study is carried out for waves passing an isolated reef terrain in a wave tank. A three-dimensional model of a representative and isolated reef terrain in the West Pacific is built. Random wave trains with various periods and wave heights are generated by a wave maker using the improved JONSWAP spectrum. It is observed that there are different kinds of generation processes and waveforms of freak waves. The freak wave factor
${H_{\rm{m}}}/{H_{\rm{s}}}$ (where${H_{\rm{m}}}$ is the maximum wave height of wave series, and${H_{\rm{s}}}$ is significant wave height) is analyzed in detail, in terms of the skewness, kurtosis and water depth, as well as the relationship between freak wave height${H_{{\rm{fr}}}}$ and skewness. The freak wave factor${H_{\rm{m}}}/{H_{\rm{s}}}$ is found to be in positive correlation with the kurtosis, while larger${H_{{\rm{fr}}}}$ tends to be related with bigger skewness. The rapid variation of water depth, such as slope and seamount, contributes to the occurrence probability of freak waves.-
Key words:
- freak waves /
- random wave /
- skewness and kurtosis /
- three-dimensional island terrain
-
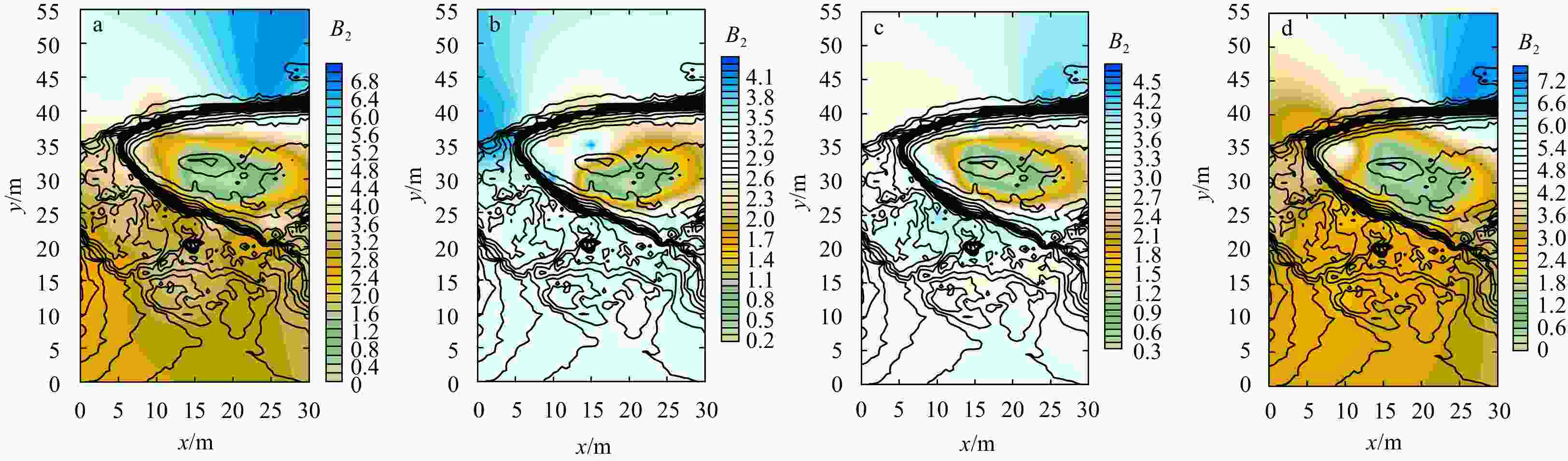
Figure 9. The variation of significant wave height along the terrain (solid curve). a.
${H_{\rm{s}}} = 6.35$ cm,${T_{\rm{s}}} = 0.87$ s,$\theta = {22.5^\circ }$ ; b.${H_{\rm{s}}} = 6.35$ cm,${T_{\rm{s}}} = 0.87$ s,$\theta = {0^\circ }$ ; c.${H_{\rm{s}}} = 3.59$ cm,${T_{\rm{s}}} = 0.8$ s,$\theta = {0^\circ }$ ; and d.${H_{\rm{s}}} = 3.59$ cm,${T_{\rm{s}}} = 0.8$ s,$\theta = - {22.5^\circ }$ .Figure 10. The variation of kurtosis along the terrain (solid curve). a.
${H_{\rm{s}}} = 6.35$ cm,${T_{\rm{s}}} = 0.87$ s,$\theta = {22.5^\circ }$ ; b.${H_{\rm{s}}} = 6.35$ cm,${T_{\rm{s}}} = 0.87$ s,$\theta = {0^\circ }$ ; c.${H_{\rm{s}}} = 3.59$ cm,${T_{\rm{s}}} = 0.8$ s,$\theta = {0^\circ }$ ; and d.${H_{\rm{s}}} = 3.59$ cm,${T_{\rm{s}}} = 0.8$ s,$\theta = - {22.5^\circ }$ .Table 1. Working conditions of irregular wave tests for 39 cases in terms of significant wave height
${H_{\rm{s}}}$ and significant period${T_{\rm{s}}}$ Case Wave
directions$(\theta )$ ${H_{\rm{s}}}$ /cm${T_{\rm{s}}}$ /sA1 ${22.5^\circ }$ 1.61 0.73 A2 3.59 0.73 A3 6.35 0.87 A4 8.05 0.87 A5 ${0^ \circ }$ 1.61 0.67, 0.73, 0.8, 0.87, 0.93, 1, 1.07, 1.2 A6 3.59 0.67, 0.73, 0.8, 0.87, 0.93, 1, 1.07, 1.14 A7 4.82 0.73 A8 6.35 0.8, 0.87, 0.93, 1, 1.07, 1.14, 1.21 A9 8.05 0.8, 0.87, 0.93, 1, 1.07, 1.14, 1.21 A10 $ - {22.5^\circ }$ 8.37 1.05 A11 1.71 0.65 A12 3.59 0.80 A13 7.08 0.91 -
Cherneva Z, Soares C G. 2014. Time-frequency analysis of the sea state with the Andrea freak wave. Nat Hazards and Earth System Sciences, 14(12): 3143–3150. doi: 10.5194/nhess-14-3143-2014 Cui Cheng, Zhang Ningchuan, Kang Haigui, et al. 2013. An experimental and numerical study of the freak wave speed. Acta Oceanologica Sinica, 32(5): 51–56. doi: 10.1007/s13131-013-0313-5 Cui Cheng, Zhang Ningchuan, Yu Yuxiu, et al. 2012. Numerical study on the effects of uneven bottom topography on freak waves. Ocean Engineering, 54: 132–141. doi: 10.1016/j.oceaneng.2012.06.021 Dean R G. 1990. Freak waves: a possible explanation. In: Tørum A, Gudmestad O T, eds. Water Wave Kinematics. Dordrecht: Springer, 609–612 Deng Yanfei, Yang Jianmin, Tian Xinliang, et al. 2016. An experimental study on deterministic freak waves: generation, propagation and local energy. Ocean Engineering, 118: 83–92. doi: 10.1016/j.oceaneng.2016.02.025 Didenkulova I. 2011. Shapes of freak waves in the coastal zone of the Baltic sea (Tallinn bay). Boreal Environment Research, 16(SA): 138–148 Dysthe K, Krogstad H E, Müller P. 2008. Oceanic rogue waves. Annual Review of Fluid Mechanics, 40(1): 287–310. doi: 10.1146/annurev.fluid.40.111406.102203 Glejin J, Kumar V S, Nair T M B, et al. 2014. Freak waves off Ratnagiri, west coast of India. Indian Journal of Geo-marine Sciences, 43(7): 1339–1342 Goda Y. 1999. A comparative review on the functional forms of directional wave spectrum. Coastal Engineering J, 41(1): 1–20. doi: 10.1142/S0578563499000024 Gramstad O, Zeng H, Trulsen K, et al. 2013. Freak waves in weakly nonlinear unidirectional wave trains over a sloping bottom in shallow water. Physics of Fluids, 25(12): 122103. doi: 10.1063/1.4847035 Haver S. 2004. A possible freak wave event measured at the Draupner jacket January 1 1995. In: Olagnon M, Prevosto M, eds. Rogue Waves 2004. Brest, France: Ifremer, 1–8 Kharif C, Pelinovsky E, Slunyaev A. 2009. Rogue Waves in the Ocean. Berlin, Heidelberg: Springer, 1–30 Lawton G. 2001. Monsters of the deep. New Scientist, 170(2297): 28–32 Li Jinxuan, Li Pengfei, Liu Shuxue. 2013. Observations of freak waves in random wave field in 2D experimental wave flume. China Ocean Engineering, 27(5): 659–670. doi: 10.1007/s13344-013-0055-3 Li Jinxuan, Yang Jiqing, Liu Shuxue, et al. 2015. Wave groupiness analysis of the process of 2D freak wave generation in random wave trains. Ocean Engineering, 104: 480–488. doi: 10.1016/j.oceaneng.2015.05.034 Liu Zanqiang, Zhang Ningchuan, Yu Yuxiu. 2011. An efficient focusing model for generation of freak waves. Acta Oceanologica Sinica, 30(6): 19–26. doi: 10.1007/s13131-011-0157-9 Lu Wenyue, Yang Jianmin, Tao Longbin. 2016. Numerical study of the energy structure of super rogue waves. Ocean Engineering, 113: 295–307. doi: 10.1016/j.oceaneng.2015.11.006 Mori N, Liu P C, Yasuda T. 2002. Analysis of freak wave measurements in the sea of Japan. Ocean Engineering, 29(11): 1399–1414. doi: 10.1016/S0029-8018(01)00073-7 Onorato M, Osborne A R, Serio M, et al. 2006. Extreme waves, modulational instability and second order theory: wave flume experiments on irregular waves. European Journal of Mechanics-B/Fluids, 25(5): 586–601. doi: 10.1016/j.euromechflu.2006.01.002 Pei Yuguo, Zhang Ningchuan, Zhang Yunqiu. 2007. Efficient generation of freak waves in laboratory. China Ocean Engineering, 21(3): 515–523 Qin Hao, Tang Wenyong, Hu Zhe, et al. 2017. Structural response of deck structures on the green water event caused by freak waves. Journal of Fluids and Structures, 68: 322–338. doi: 10.1016/j.jfluidstructs.2016.11.009 Sergeeva A, Pelinovsky E, Talipova T. 2011. Nonlinear random wave field in shallow water: variable Korteweg-de Vries framework. Natural Hazards and Earth System Sciences, 11(2): 323–330. doi: 10.5194/nhess-11-323-2011 Shemer L, Sergeeva A. 2009. An experimental study of spatial evolution of statistical parameters in a unidirectional narrow-banded random wavefield. Journal of Geophysical Research: Oceans, 114(C1): C01015 Slunyaev A, Didenkulova I, Pelinovsky E. 2011. Rogue waters. Contemporary Physics, 52(6): 571–590. doi: 10.1080/00107514.2011.613256 Soares C G, Cherneva Z, Antão E M. 2003. Characteristics of abnormal waves in North Sea storm sea states. Applied Ocean Research, 25(6): 337–344. doi: 10.1016/j.apor.2004.02.005 Tayfun M A, Fedele F. 2007. Wave-height distributions and nonlinear effects. Ocean Engineering, 34(11–12): 1631–1649. doi: 10.1016/j.oceaneng.2006.11.006 Toffoli A, Bitner-Gregersen E, Onorato M, et al. 2008. Wave crest and trough distributions in a broad-banded directional wave field. Ocean Engineering, 35(17–18): 1784–1792. doi: 10.1016/j.oceaneng.2008.08.010 Toffoli A, Cavaleri L, Babanin A V, et al. 2011. Occurrence of extreme waves in three-dimensional mechanically generated wave fields propagating over an oblique current. Natural Hazards and Earth System Sciences, 11(3): 895–903. doi: 10.5194/nhess-11-895-2011 Toffoli A, Waseda T, Houtani H, et al. 2015. Rogue waves in opposing currents: an experimental study on deterministic and stochastic wave trains. Journal of Fluid Mechanics, 769: 277–297. doi: 10.1017/jfm.2015.132 Trulsen K, Zeng H, Gramstad O. 2012. Laboratory evidence of freak waves provoked by non-uniform bathymetry. Physics of Fluids, 24(9): 097101. doi: 10.1063/1.4748346 Veltcheva A D, Soares C G. 2012. Analysis of abnormal wave groups in Hurricane Camille by the Hilbert Huang Transform method. Ocean Engineering, 42: 102–111. doi: 10.1016/j.oceaneng.2011.12.013 Waseda T, Kinoshita T, Tamura H. 2009. Evolution of a random directional wave and freak wave occurrence. Journal of Physical Oceanography, 39(3): 621–639. doi: 10.1175/2008JPO4031.1 Zeng H, Trulsen K. 2012. Evolution of skewness and kurtosis of weakly nonlinear unidirectional waves over a sloping bottom. Natural Hazards and Earth System Sciences, 12(3): 631–638. doi: 10.5194/nhess-12-631-2012 Zhang Yunqiu, Zhang Ningchuan, Hu Jinpeng. 2007. Numerical simulation and mechanism analysis of freak waves. Acta Oceanologica Sinica, 26(5): 116–124 -









 下载:
下载:
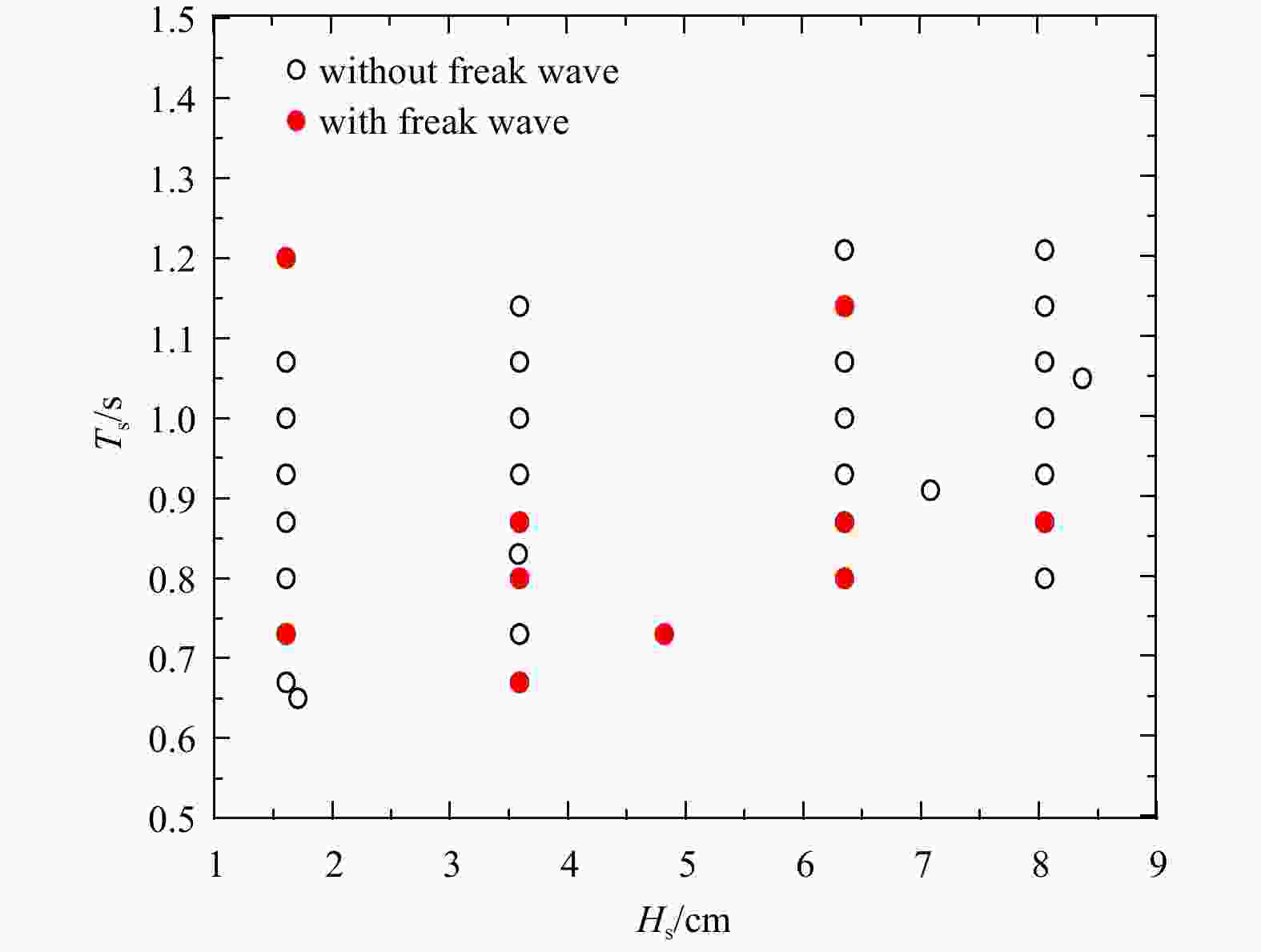






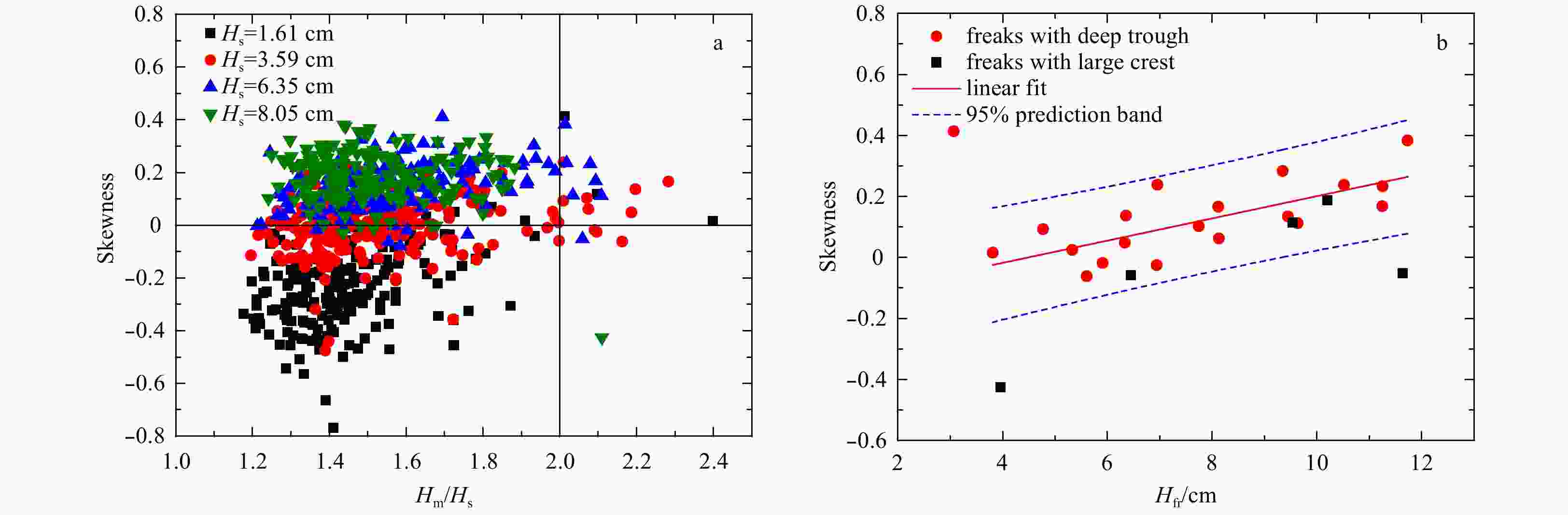



 ) represents cases with freak waves, the black solid (
) represents cases with freak waves, the black solid ( ) cases without freak waves.
) cases without freak waves.