Sea surface temperature retrieval based on simulated microwave polarimetric measurements of a one-dimensionalsynthetic aperture microwave radiometer
-
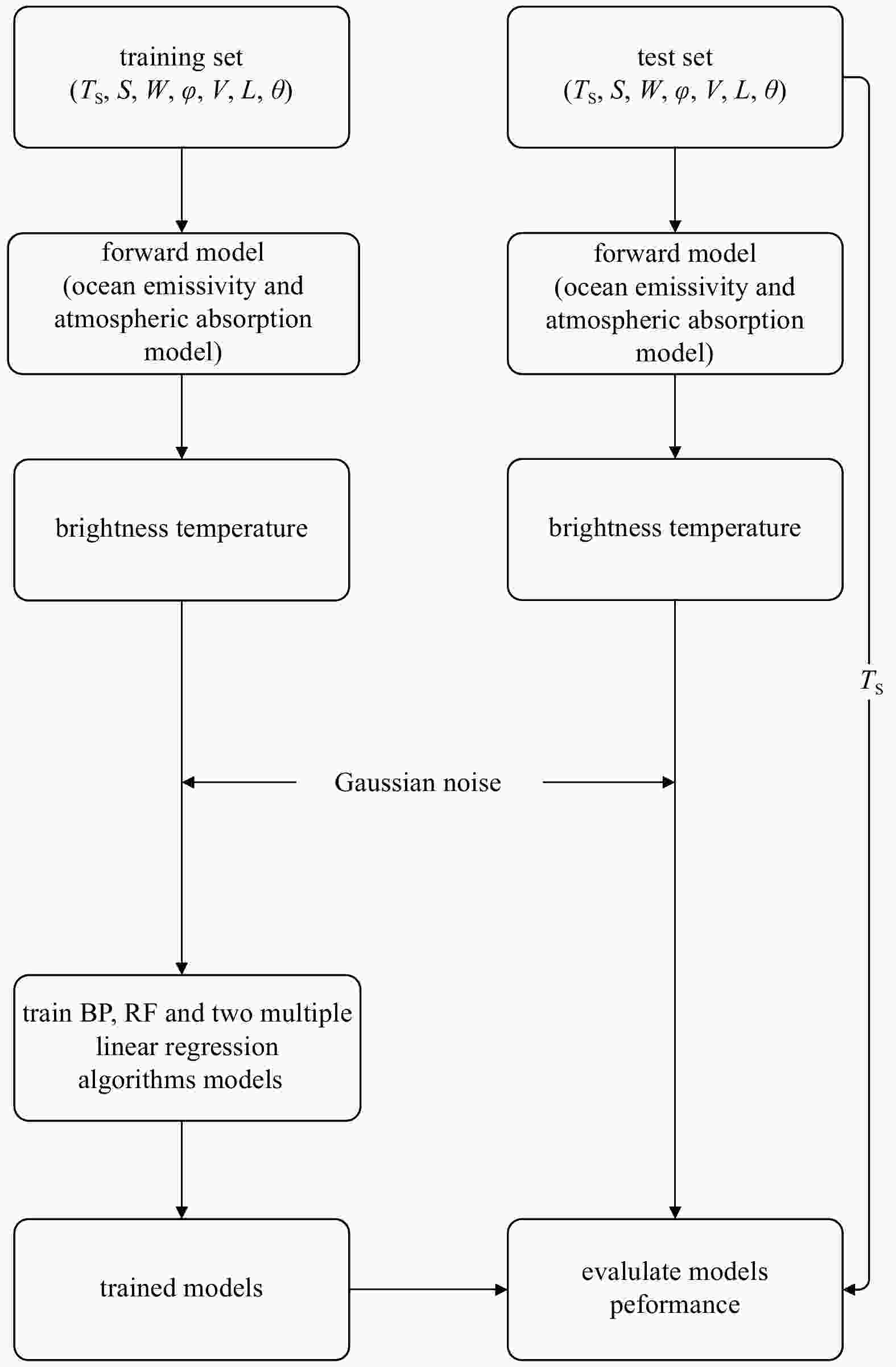
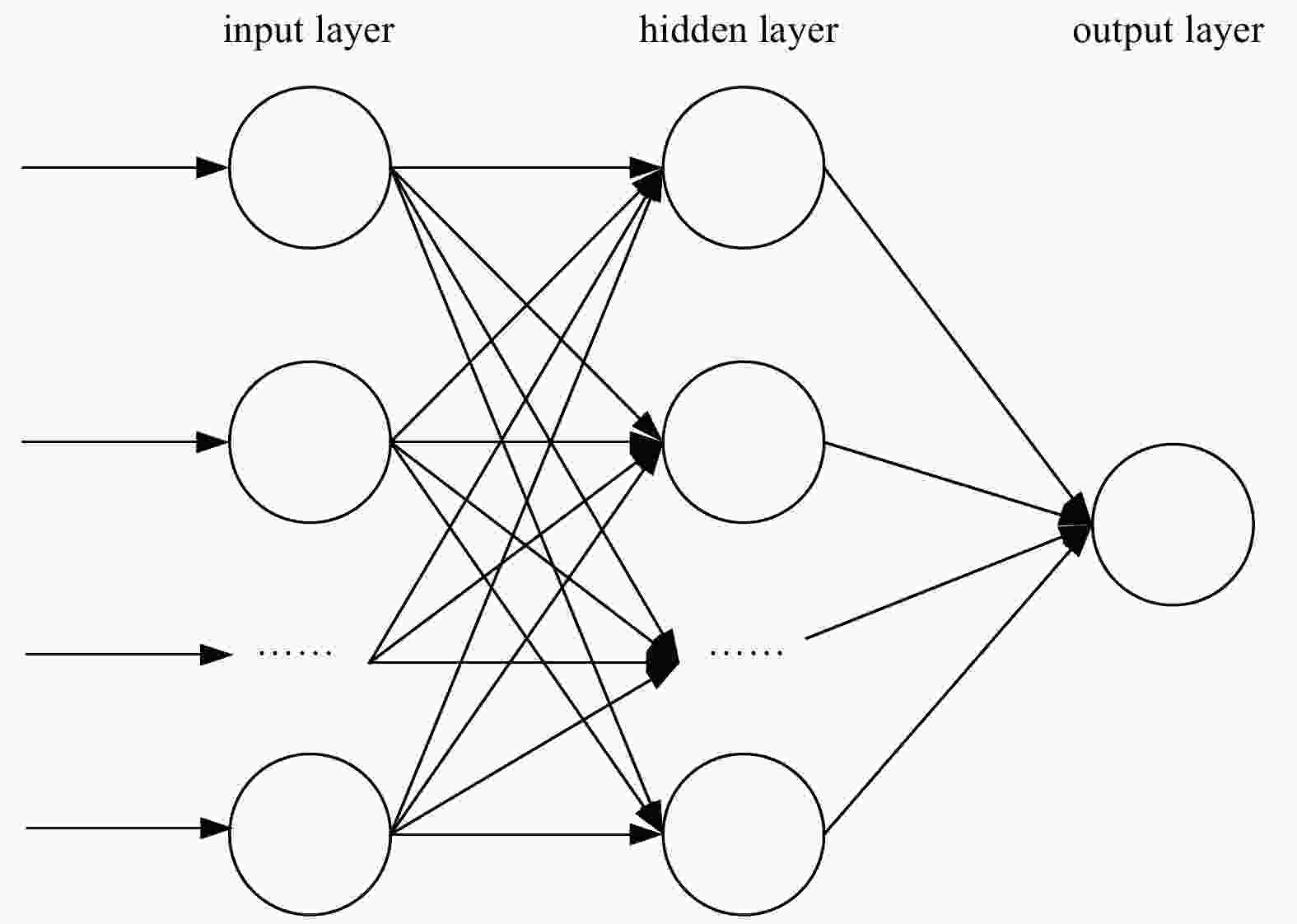
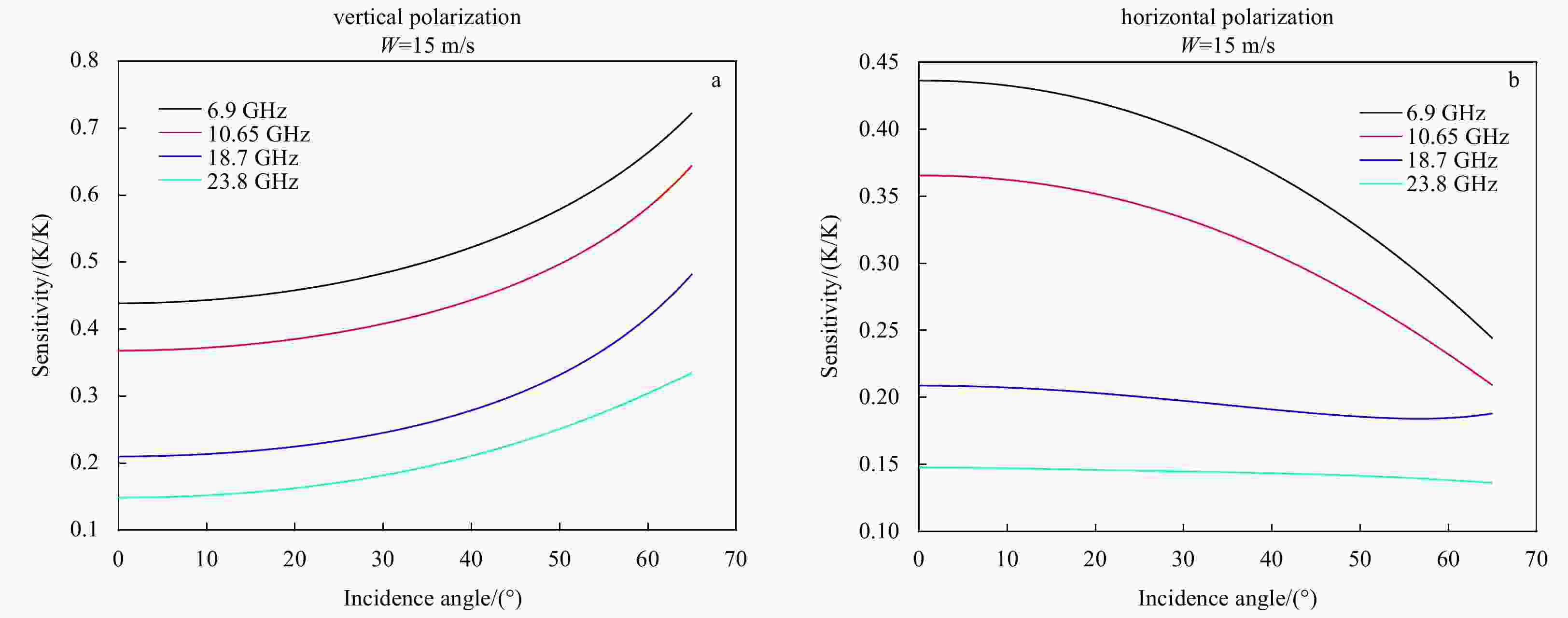
Abstract: Compared with traditional real aperture microwave radiometers, one-dimensional synthetic aperture microwave radiometers have higher spatial resolution. In this paper, we proposed to retrieve sea surface temperature using a one-dimensional synthetic aperture microwave radiometer that operates at frequencies of 6.9 GHz, 10.65 GHz, 18.7 GHz and 23.8 GHz at multiple incidence angles. We used the ERA5 reanalysis data provided by the European Centre for Medium-Range Weather Forecasts and a radiation transmission forward model to calculate the model brightness temperature. The brightness temperature measured by the spaceborne one-dimensional synthetic aperture microwave radiometer was simulated by adding Gaussian noise to the model brightness temperature. Then, a backpropagation (BP) neural network algorithm, a random forest (RF) algorithm and two multiple linear regression algorithms (RE1 and RE2) were developed to retrieve sea surface temperature from the measured brightness temperature within the incidence angle range of 0°–65°. The results show that the retrieval errors of the four algorithms increase with the increasing Gaussian noise. The BP achieves the lowest retrieval errors at all incidence angles. The retrieval error of the RE1 and RE2 decrease first and then increase with the incidence angle and the retrieval error of the RF is contrary to that of RE1 and RE2.
-
Figure 2. The schematic diagram of the incidence angle of a one-dimensional synthetic aperture radiometer.
Figure 3. Distribution histogram of environment parameters. a. Sea surface temperature, b. wind direction, c. wind speed, d. total column cloud water vapor content, and e. total column cloud liquid water content.
Figure 6. The relationship between sensitivity of brightness temperature to SST and incidence angle.
Figure 7. The relationship between sensitivity of brightness temperature to SST and SST at
$\theta \!=\! {30^ \circ }$ .
Figure 9. Relationships between the retrieval errors and sea surface temperature when the added noise is 0.50 K and
$\theta \!=\! 30^\circ$ .
Figure 10. Scatterplots of retrieval sea surface temperature and true sea surface temperature for Gaussian error of 0.5 K and
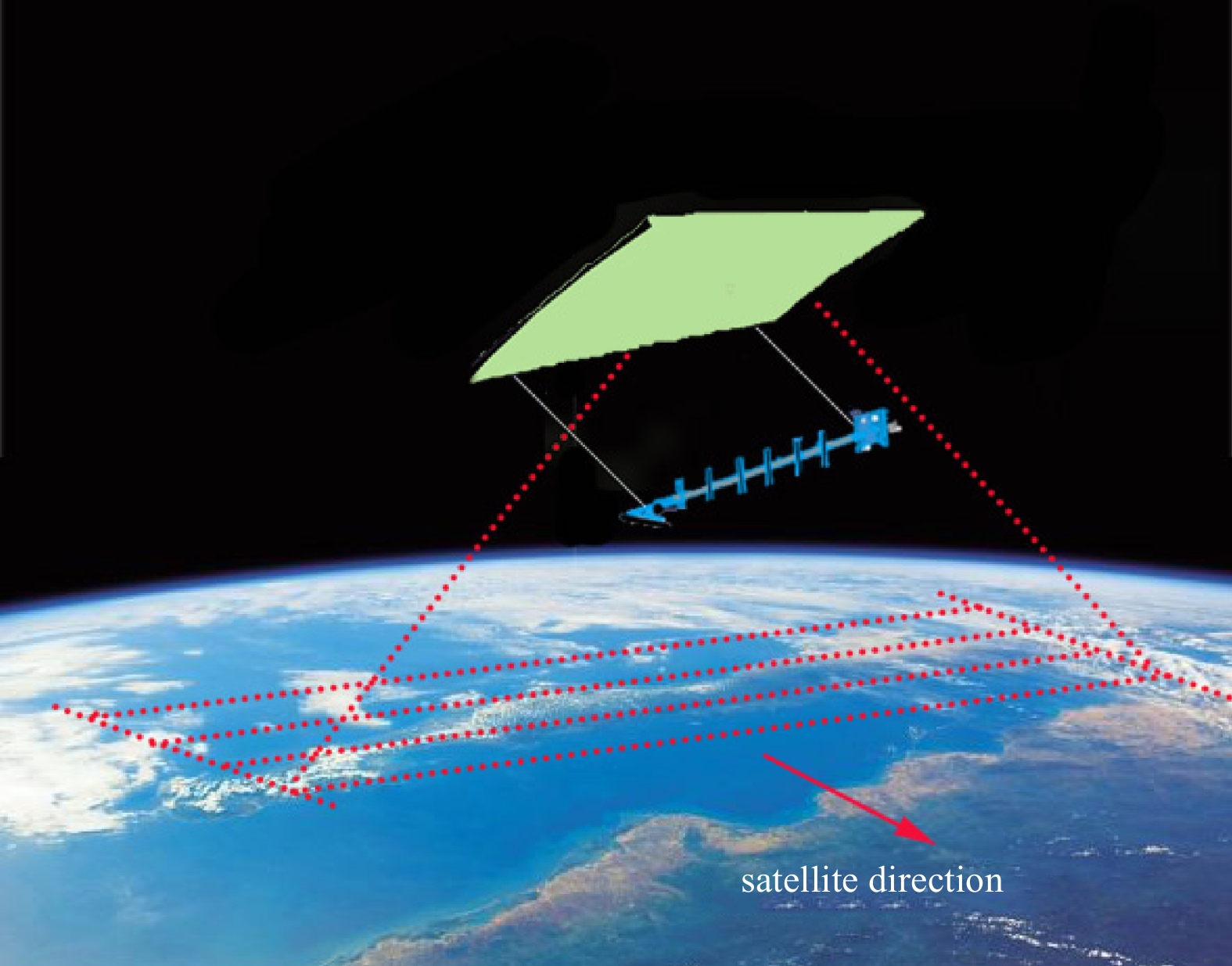
$\theta \!= \!30^\circ$ .Table 1. Parameters of the one-dimensional synthetic aperture radiometer
Parameter Values Frequency/GHz 6.9 Bandwidth/MHz 200 Polarization modes vertical and horizontal polarization Integral time/s 0.5 Number of antenna elements 55 Minimum spacing between antenna elements 0.73λ Angular range of the field of view –43° to 43° Angular resolution 0.43° Antenna element positions [0 1 2 3 7 11 12 14 21 24 26 28 38 43 58 59 60 65 68 70 73 75 76 78 83 86 88 93 101 103 105 112 118
121 122 123 132 133 134 137 147 148 153 156 164 166 172 173 174 175 178 180 181 182 183]Parabolic size 12 m×10 m Spatial resolution at nadir/km 5 Range of incidence angle θ with vertical observation –51° to 51° 
下载: 导出CSV
Table 2. Geophysical parameter values for the background field used in the sensitivity analysis
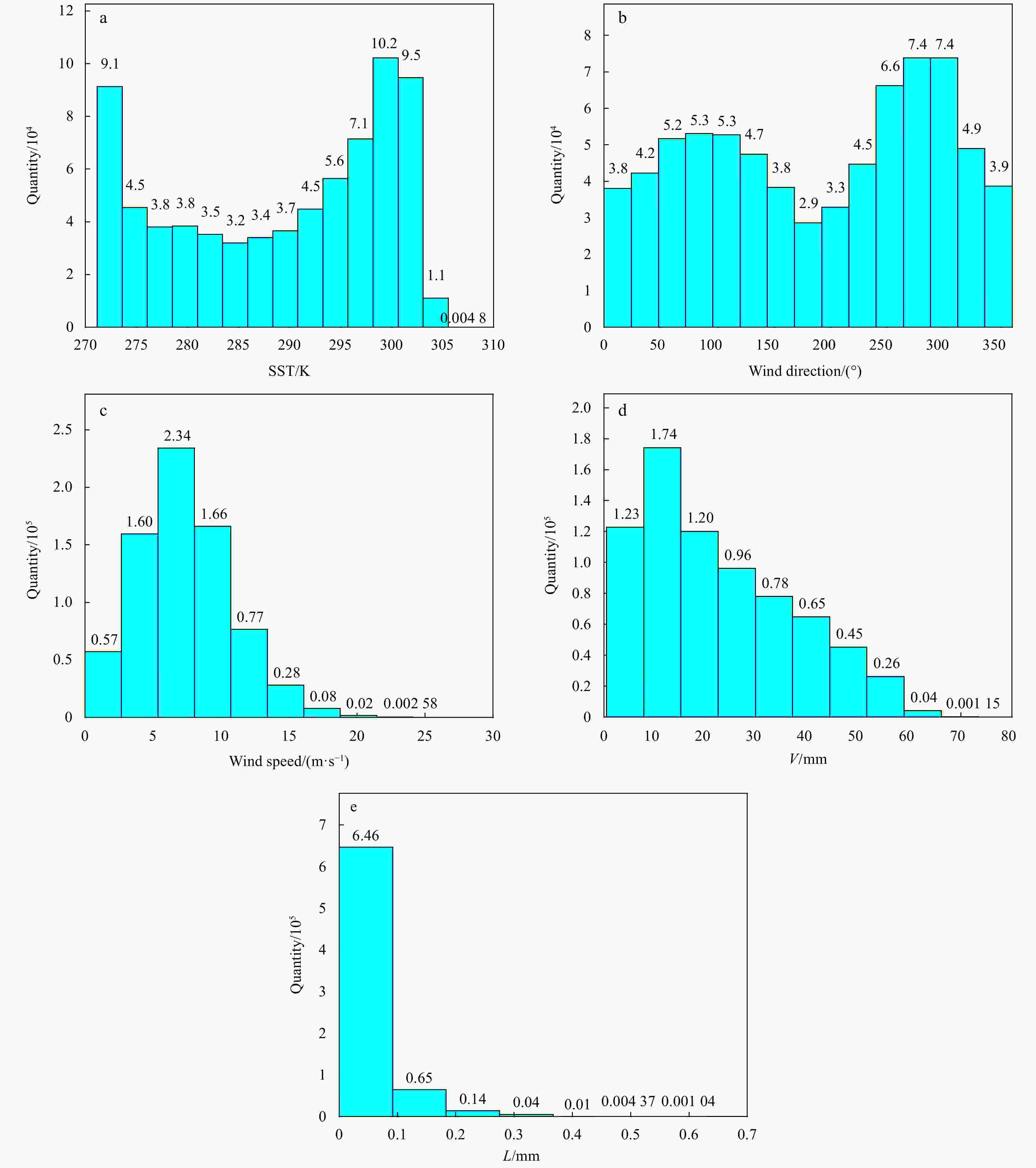
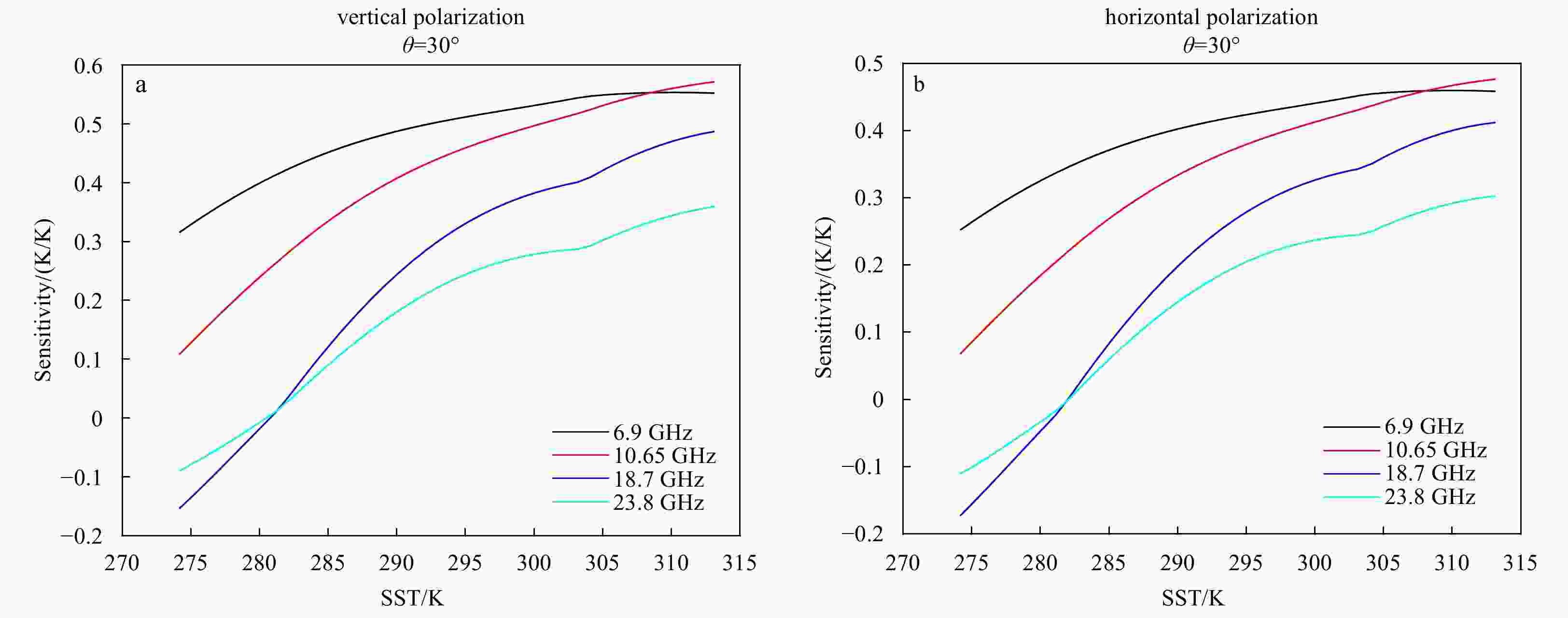
Scene S TS/K W/(m·s–1 ) φ/(°) V/mm L/mm Scene2 35 273.15–313.15 15 30 30 0.1
下载: 导出CSV
Table 3. Mean RMS errors, where the top values are the training set and the bottom values are the test set
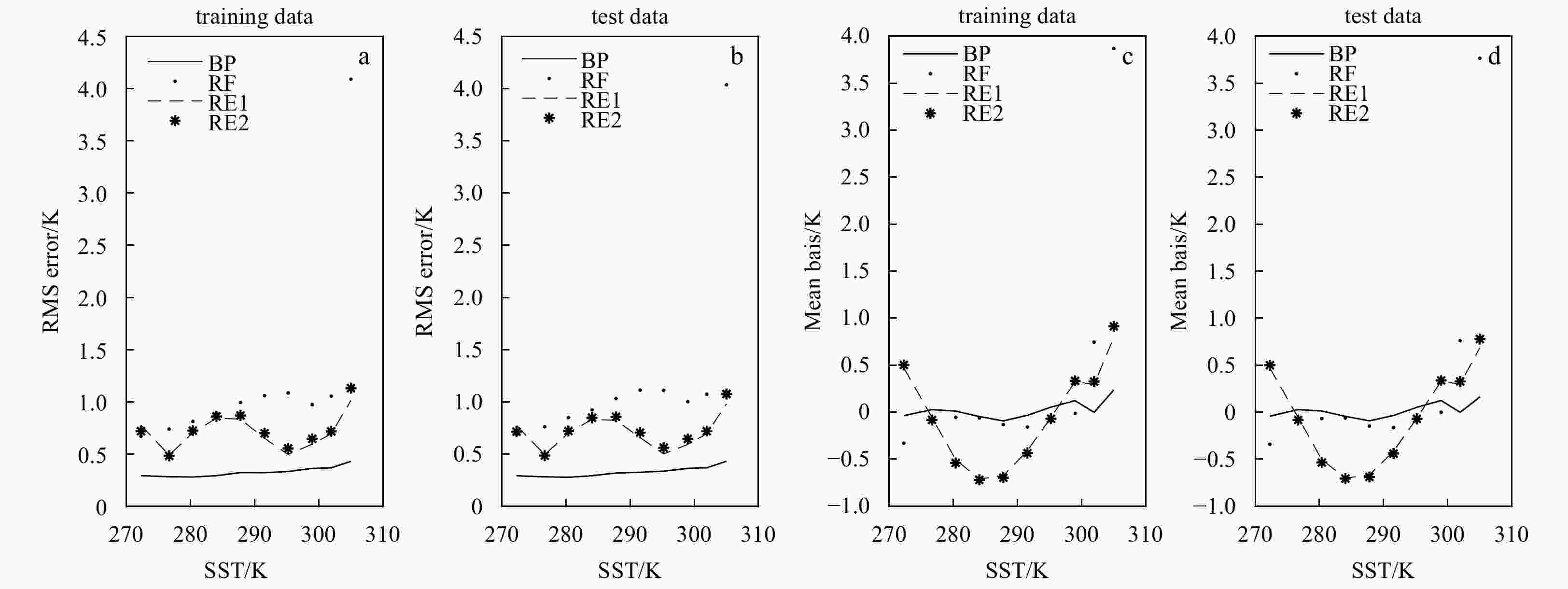
Noise/K Mean RMS error/K BP RF RE1 RE2 0.25 0.30 0.76 0.60 0.61 0.30 0.78 0.60 0.61 0.50 0.42 0.90 0.68 0.69 0.42 0.92 0.68 0.68 0.75 0.50 1.04 0.74 0.75 0.51 1.07 0.74 0.75
下载: 导出CSV
Table 4. The average mean biases, where the top values are the training set and the bottom values are the test set
Noise/K Mean bias/K BP RF RE1 RE2 0.25 −1.0×10−4 −6.0×10−4 2.1×10−4 −1.5×10−4 −1.1×10–4 −0.001 −1.2×10−3 −1.3×10−3 0.50 −3.7×10−4 −6.0×10−4 −3.2×10−5 7.1×10−5 −5.7×10−4 −4.7×10−4 −7.7×10−4 −8.9×10−4 0.75 −0.005 −5.4×10−4 −1.2×10−5 −2.6×10−5 −0.005 −6.4×10−4 6.6×10−4 −6.6×10−4
下载: 导出CSV
Table 5. SST interval and sample size for each interval in the training set and the corresponding RMS error and mean bias
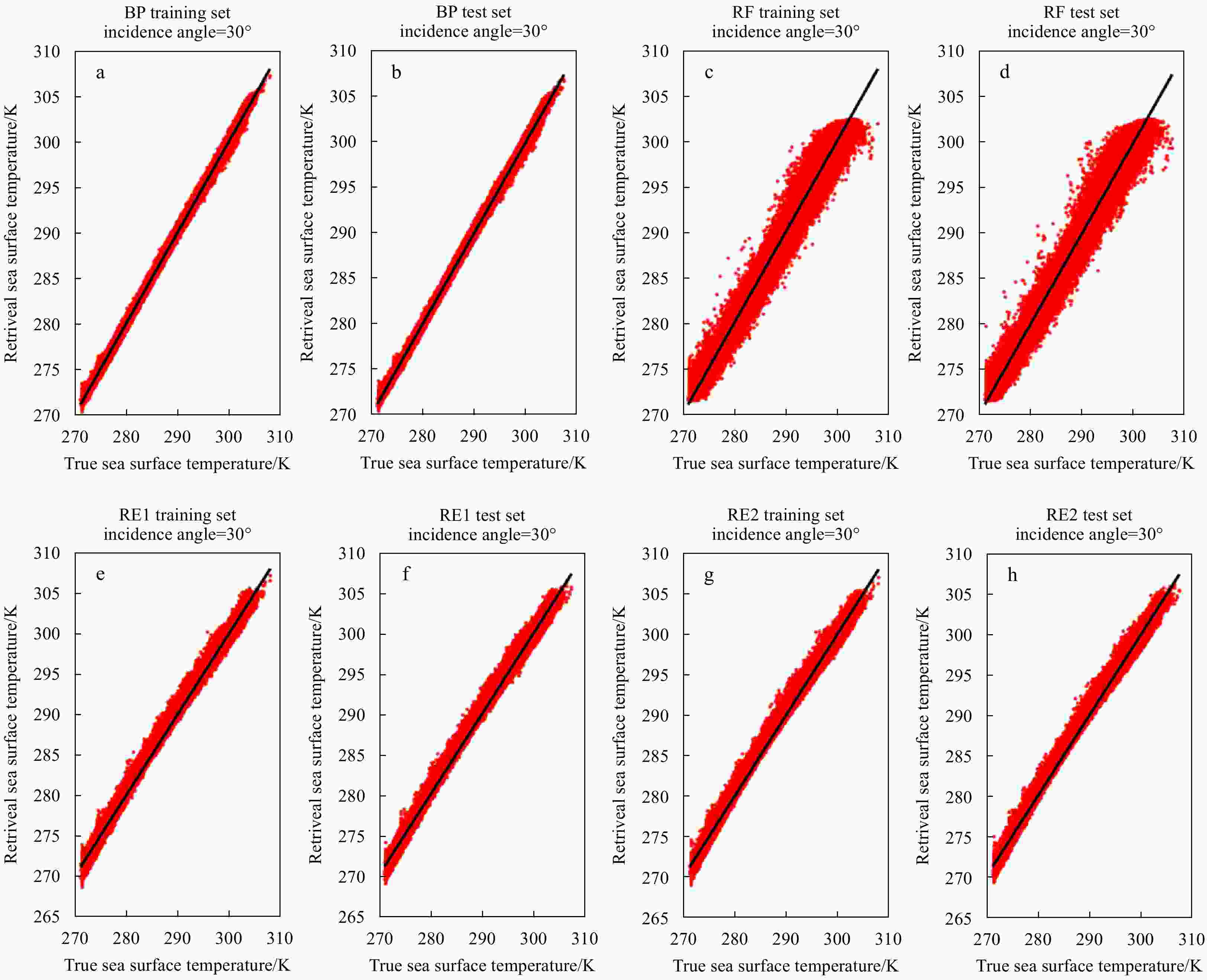
SST/K N RMS error and mean bias/K BP RF RE1 RE2 271.15–274.84 58 459 0.29/−0.03 0.67/−0.32 0.77/0.47 0.72/0.50 274.85–278.53 29 087 0.28/0.02 0.74/−0.09 0.49/−0.05 0.48/−0.08 278.54–282.21 28 518 0.28/0.01 0.81/−0.05 0.70/−0.50 0.72/−0.53 282.22–285.90 24 194 0.29/−0.04 0.89/−0.06 0.84/−0.71 0.86/−0.71 285.91–289.59 25 850 0.32/−0.09 0.99/−0.13 0.83/−0.67 0.87/−0.69 289.60–293.27 31 802 0.32/−0.03 1.06/−0.15 0.65/−0.40 0.70/−0.43 293.28–296.96 44 625 0.33/0.05 1.08/−0.09 0.49/−0.05 0.55/−0.06 296.97–300.65 70 249 0.36/0.10 0.97/−0.01 0.59/0.32 0.64/0.33 300.66–304.33 52 658 0.37/0.001 1.05/0.74 0.66/0.29 0.71/0.32 304.34–308.02 154 0.36/0.20 4.09/3.86 1.01/0.79 1.13/0.91 All 365 624 0.38/−0.01 0.93/0.004 0.67/0.00 0.69/0.00 Note: The RMS error and the mean bias are separated by “/”.
下载: 导出CSV
Table 6. SST interval and sample size for each interval in the test set and the corresponding RMS error and mean bias
SST/K N RMS error and mean bias/K BP RF RE1 RE2 271.15–274.84 58 001 0.29/−0.04 0.69/−0.34 0.78/0.47 0.72/0.50 274.85–278.53 29 091 0.28/0.03 0.76/−0.09 0.49/−0.06 0.49/−0.08 278.54–282.21 28 662 0.28/0.01 0.85/−0.07 0.70/−0.50 0.72/−0.53 282.22–285.90 24 139 0.29/−0.04 0.92/−0.06 0.84/−0.70 0.85/−0.71 285.91–289.59 25 993 0.32/−0.09 1.03/−0.15 0.82/−0.67 0.86/−0.69 289.60–293.27 31 739 0.33/−0.03 1.11/−0.16 0.66/−0.41 0.71/−0.44 293.28–296.96 44 534 0.34/0.05 1.11/−0.09 0.50/−0.06 0.56/−0.07 296.97–300.65 70 595 0.36/0.13 1.01/0.00 0.59/0.33 0.65/0.34 300.66–304.33 52 703 0.37/0.00 1.07/0.76 0.70/0.30 0.72/0.33 304.34–308.02 167 0.43/0.16 4.03/3.76 0.98/0.69 1.07/0.78 All 365 624 0.39/−0.01 0.97/0.004 0.67/0.00 0.69/−0.001 Note: The RMS error and the mean bias are separated by “/”.
下载: 导出CSV
-
[1] Aires F, Prigent C, Rossow W B, et al. 2001. A new neural network approach including first guess for retrieval of atmospheric water vapor, cloud liquid water path, surface temperature, and emissivities over land from satellite microwave observations. Journal of Geophysical Research, 106(D4): 14887–14907 [2] Alsweiss S O, Jelenak Z, Chang P S. 2017. Remote sensing of sea surface temperature using AMSR-2 measurements. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 10(9): 3948–3954 [3] Bettenhausen M H, Smith C K, Bevilacqua R M, et al. 2006. A nonlinear optimization algorithm for WindSat wind vector retrievals. IEEE Transactions on Geoscience and Remote Sensing, 44(3): 597–610. doi: 10.1109/TGRS.2005.862504 [4] Bobylev L P, Zabolotskikh E V, Mitnik L M, et al. 2010. Atmospheric water vapor and cloud liquid water retrieval over the Arctic ocean using satellite passive microwave sensing. IEEE Transactions on Geoscience and Remote Sensing, 48(1): 283–294. doi: 10.1109/TGRS.2009.2028018 [5] Brown S T, Ruf C S, Lyzenga D R. 2006. An emissivity-based wind vector retrieval algorithm for the WindSat polarimetric radiometer. IEEE Transactions on Geoscience and Remote Sensing, 44(3): 611–621. doi: 10.1109/TGRS.2005.859351 [6] Camps A, Park H, Bandeiras J, et al. 2016. Microwave imaging radiometers by aperture synthesis—Performance simulator (Part 1): Radiative transfer module. Journal of Imaging, 2(2): 17. doi: 10.3390/jimaging2020017 [7] Chelton D B, Wentz F J. 2005. Global microwave satellite observations of sea surface temperature for numerical weather prediction and climate research. Bulletin of the American Meteorological Society, 86(8): 1097–1116. doi: 10.1175/BAMS-86-8-1097 [8] Corbella I, Duffo N, Vall-Llossera M, et al. 2004. The visibility function in interferometric aperture synthesis radiometry. IEEE Transactions on Geoscience and Remote Sensing, 42(8): 1677–1682. doi: 10.1109/TGRS.2004.830641 [9] Emanuel A K. 1999. Thermodynamic control of hurricane intensity. Nature, 401(6754): 665–669. doi: 10.1038/44326 [10] Goodberlet M A, Swift C T, Wilkerson J C. 1990. Ocean surface wind speed measurements of the special sensor microwave/imager (SSM/I). IEEE Transactions on Geoscience and Remote Sensing, 28(5): 823–828. doi: 10.1109/36.58969 [11] Hollinger J P. 1971. Passive microwave measurements of sea surface roughness. IEEE Transactions on Geoscience Electronics, 9(3): 165–169. doi: 10.1109/TGE.1971.271489 [12] Jung T, Ruprecht E, Wagner F. 1998. Determination of cloud liquid water path over the oceans from special sensor microwave/imager (SSM/I) data using neural networks. Journal of Applied Meteorology and Climatology, 37(8): 832–844. doi: 10.1175/1520-0450(1998)037<0832:DOCLWP>2.0.CO;2 [13] Kilic L, Prigent C, Aires F, et al. 2018. Expected performances of the copernicus imaging microwave radiometer (CIMR) for an all-weather and high spatial resolution estimation of ocean and sea ice parameters. Journal of Geophysical Research: Oceans, 123(10): 7564–7580. doi: 10.1029/2018JC014408 [14] Koner P K, Harris A, Maturi E. 2015. A physical deterministic inverse method for operational satellite remote sensing: An application for sea surfacetemperature retrievals. IEEE Transactions on Geoscience and Remote Sensing, 53(11): 5872–5888. doi: 10.1109/TGRS.2015.2424219 [15] Krasnopolsky V M, Gemmill W H, Breaker L C. 2000. A neural network multiparameter algorithm for SSM/I ocean retrievals: Comparisons and validations. Remote Sensing of Environment, 73(2): 133–142. doi: 10.1016/S0034-4257(00)00088-2 [16] Le Vine D M. 1990. The sensitivity of synthetic aperture radiometers for remote sensing applications from space. Radio Science, 25(4): 441–453. doi: 10.1029/RS025i004p00441 [17] Le Vine D M, Griffis A J, Swift C T, et al. 1994. ESTAR: A synthetic aperture microwave radiometer for remote sensing applications. Proceedings of the IEEE, 82(12): 1787–1801. doi: 10.1109/5.338071 [18] Le Vine D M, Kao M, Swift C T, et al. 1990. Initial results in the development of a synthetic aperture microwave radiometer. IEEE Transactions on Geoscience and Remote Sensing, 28(4): 614–619. doi: 10.1109/TGRS.1990.572965 [19] Le Vine D M, Swift C T, Haken M. 2001. Development of the synthetic aperture microwave radiometer, ESTAR. IEEE Transactions on Geoscience and Remote Sensing, 39(1): 199–202. doi: 10.1109/36.898685 [20] Lim B H. 2009. The design and development of a geostationary synthetic thinned aperture radiometer [dissertation]. Michigan: The University of Michigan [21] Martin-Neira M, Menard Y, Goutoule J M, et al. 1994. MIRAS, a two-dimensional aperture synthesis radiometer. In: Proceeding of the 1994 IEEE International Geoscience and Remote Sensing Symposium. Pasadena, CA, USA: IEEE, 1323-1325 [22] Martin-Neira M, Ribo S, Martin-Polegre A J. 2002. Polarimetric mode of MIRAS. IEEE Transactions on Geoscience and Remote Sensing, 40(8): 1755–1768. doi: 10.1109/TGRS.2002.802489 [23] Mätzler C. 2006. Thermal Microwave Radiation: Applications for Remote Sensing. London: The Institution of Engineering and Technology [24] McClain E P, Pichel W G, Walton C C. 1985. Comparative performance of AVHRR-based multichannel sea surface temperatures. Journal of Geophysical Research: Oceans, 90(C6): 11587–11601. doi: 10.1029/JC090iC06p11587 [25] McPhaden M J. 1999. Genesis and evolution of the 1997–98 El Niño. Science, 283(5404): 950–954. doi: 10.1126/science.283.5404.950 [26] Meissner T, Wentz F J. 2004. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Transactions on Geoscience and Remote Sensing, 42(9): 1836–1849. doi: 10.1109/TGRS.2004.831888 [27] Meissner T, Wentz F. 2005. Ocean retrievals for WindSat: Radiative transfer model, algorithm, validation. In: Proceedings of OCEANS 2005 MTS/IEEE. Washington, DC, USA: IEEE, 130–133 [28] Meissner T, Wentz F J. 2009. Wind-vector retrievals under rain with passive satellite microwave radiometers. IEEE Transactions on Geoscience and Remote Sensing, 47(9): 3065–3083. doi: 10.1109/TGRS.2009.2027012 [29] Meissner T, Wentz F J. 2012. The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles. IEEE Transactions on Geoscience and Remote Sensing, 50(8): 3004–3026. doi: 10.1109/TGRS.2011.2179662 [30] Obligis E, Labroue S, Amar A, et al. 2005. Neural networks to retrieve sea surface salinity from SMOS brightness temperatures. In: Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium. Seoul, South Korea: IEEE, 2568–2571 [31] Ruf C S, Swift C T, Tanner A B, et al. 1988. Interferometric synthetic aperture microwave radiometry for the remote sensing of the earth. IEEE Transactions on Geoscience and Remote Sensing, 26(5): 597–611. doi: 10.1109/36.7685 [32] Schanda E. 1979. Multiple wavelength aperture synthesis for passive sensing of the earth's surface. In: 1979 Antennas and Propagation Society International Symposium. Seattle, WA, USA: IEEE, 762–763 [33] Stogryn A. 1967. The apparent temperature of the sea at microwave frequencies. IEEE Transactions on Antennas and Propagation, 15(2): 278–286. doi: 10.1109/TAP.1967.1138900 [34] Ulaby F T, Dobson M C, Brunfeldt D R. 1983. Improvement of moisture estimation accuracy of vegetation-covered soil by combined active/passive microwave remote sensing. IEEE Transactions on Geoscience and Remote Sensing, GE-21(3): 300–307. doi: 10.1109/TGRS.1983.350557 [35] Wang Rui, Shi Shunwen, Yan Wei, et al. 2014. Sea surface wind retrieval from polarimetric microwave radiometer in typhoon area. Chinese Journal of Geophysics (in Chinese), 57(3): 738–751 [36] Wang Naiyu, Chang P S, Bettenhausen M, et al. 2005. WindSat physically based forward model: atmospheric component. In: Proceedings of SPIE—The International Society for Optical Engineering, vol. 5656, Active and Passive Remote Sensing of the Oceans: 104–110, doi: 10.1117/12.578811 [37] Wentz F J, Meissner T. 2000. Algorithm theoretical basis document (ATBD). Version 2: AMSR Ocean Algorithm. Santa Rosa, CA: Remote Sensing Systems -
点击查看大图
图(10) / 表(6)
计量
- 文章访问数: 387
- HTML全文浏览量: 130
- PDF下载量: 6
- 被引次数: 0
