A two-stage inflation method in parameter estimation to compensate for constant parameter evolution in Community Earth System Model
-
Abstract: Parameter estimation is defined as the process to adjust or optimize the model parameter using observations. A long-term problem in ensemble-based parameter estimation methods is that the parameters are assumed to be constant during model integration. This assumption will cause underestimation of parameter ensemble spread, such that the parameter ensemble tends to collapse before an optimal solution is found. In this work, a two-stage inflation method is developed for parameter estimation, which can address the collapse of parameter ensemble due to the constant evolution of parameters. In the first stage, adaptive inflation is applied to the augmented states, in which the global scalar parameter is transformed to fields with spatial dependence. In the second stage, extra multiplicative inflation is used to inflate the scalar parameter ensemble to compensate for constant parameter evolution, where the inflation factor is determined according to the spread growth ratio of model states. The observation system simulation experiment with Community Earth System Model (CESM) shows that the second stage of the inflation scheme plays a crucial role in successful parameter estimation. With proper multiplicative inflation factors, the parameter estimation can effectively reduce the parameter biases, providing more accurate analyses.
-
Key words:
- parameter estimation /
- data assimilation /
- inflation /
- CESM /
- EnKF
-
Figure 1. Flow diagram of OSSE for state and parameter estimation. The unit of bckgrnd-vdc is cm2/s.
Figure 2. TS profile locations (a) and depths (b) of the period from January 1, 2010 to January 10, 2010. For a better display, only the depths of the first 500 observations are shown in b.
Figure 3. SST spread (left) and SSS spread (right) of the 1st (a, b), 4th (c, d), 7th (e, f), 10th (g, h) month from the parameter sensitivity experiment.
Figure 4. RMSEs of prior and posterior innovations of the temperature (left) and salinity (right) for depths 10 m (a, b), 50 m (c, d), 200 m (e, f), and 1 000 m (g, h).
Figure 5. RMSE of SST (a,b), SSS (c,d), and SSH (e,f) from control run (left) and state estimation (right) of the first 6 months.
Figure 6. The ratio of posterior error standard deviation to prior error standard deviation of the parameter ensemble (a); the posterior ensemble member 1–3 (b–d). The quantities are computed for the first parameter estimation step.
Figure 7. The spatial varying inflation values for temperature (left) and salinity (right) in 5 m (a, b), 100 m (c, d) and 200 m (e, f) depth; the inflation values for the two-dimensional parameter field for the first analysis step (g).
Figure 8. The evolution of the parameter mean (red solid line) plus/minus one standard deviation (red dotted lines) over the data assimilation period (a); the parameter error (red line) and ensemble spread (green line) over the data assimilation period (b).
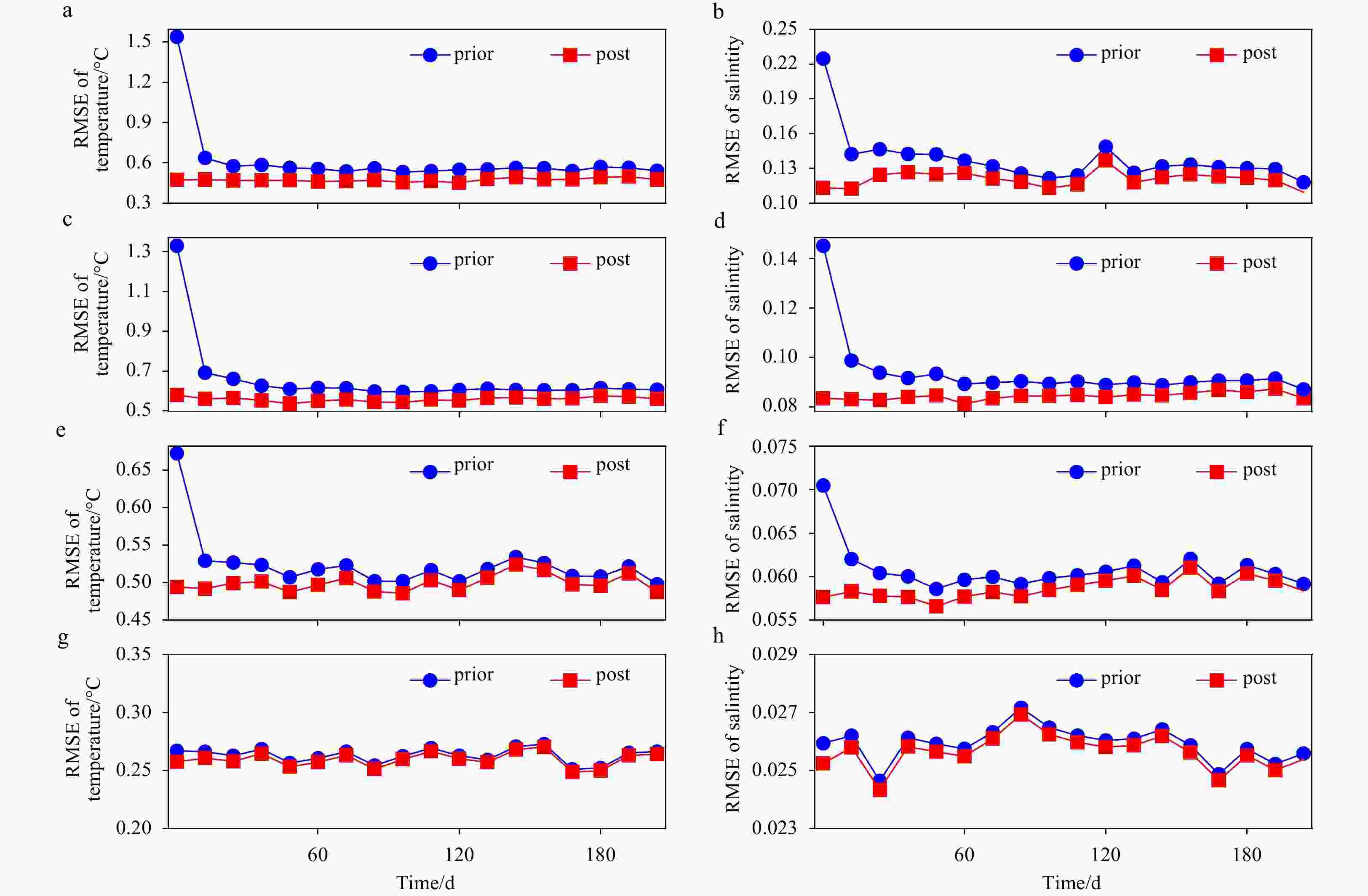
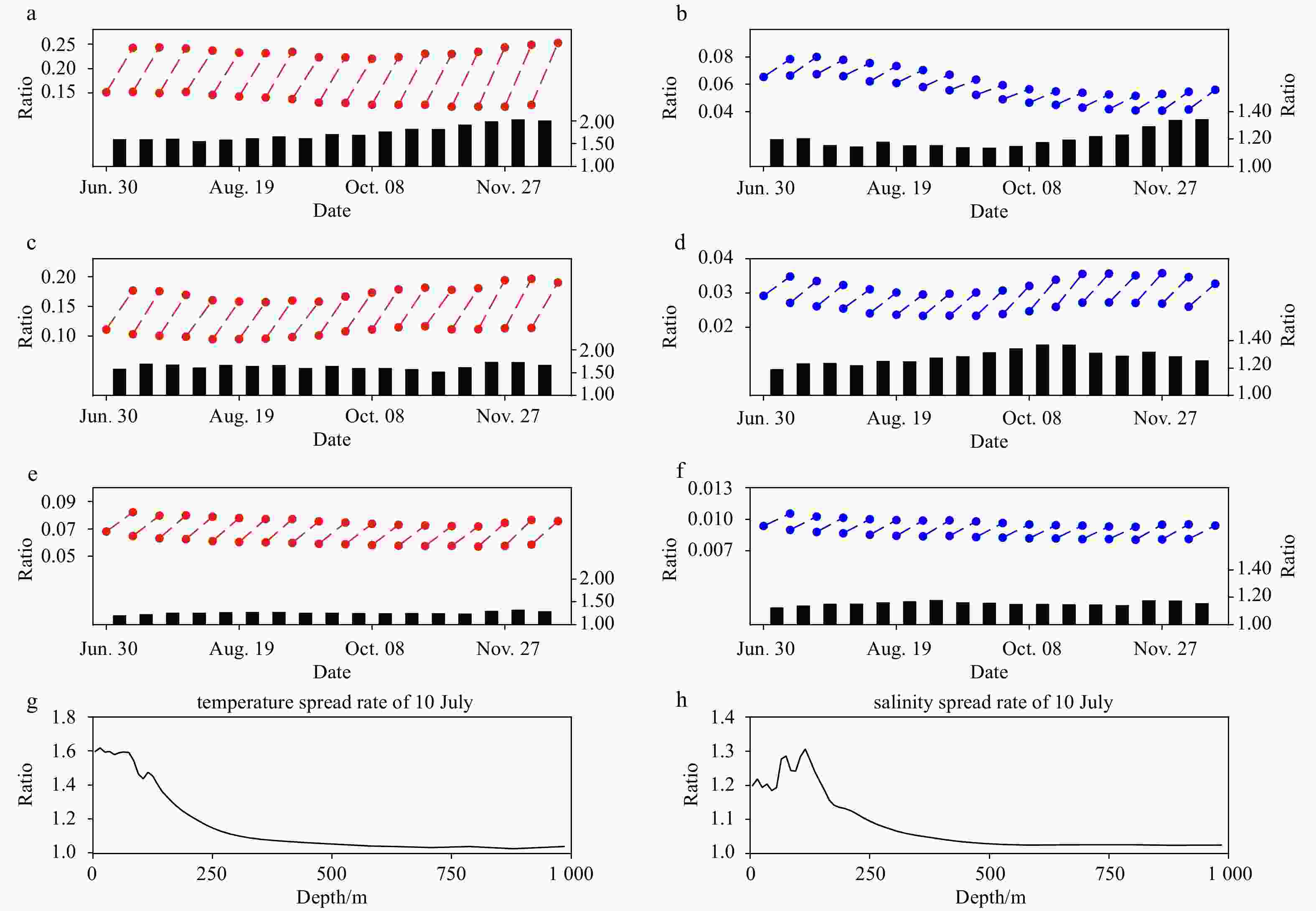
Figure 9. The global mean temperature (left) and salinity (right) spread in each data assimilation step at the depth 5 m (a, b), 50 m (c, d), and 200 m (e, f), each dashed line connects the posterior of the previous step and the prior of the current step. And the temperature (g) and salinity (h) spread growth ratio at the first step.
Figure 10. The evolution of the parameter mean (red solid line) and spread (red dotted lines) over the data assimilation period using extra parameter inflation with
$ \mathrm{\alpha }=1.1 $ (a), 1.2 (b), 1.3 (c), and 1.5 (d), respectively.
Figure 11. The temperature (upper) and salinity (bottom) RMSE for the last 6 months of the 2nd year using the data assimilation results from parameter estimation and pure state estimation, respectively.
-
[1] Aksoy A, Zhang Fuqing, Nielsen-Gammon J W. 2006. Ensemble-based simultaneous state and parameter estimation with MM5. Geophysical Research Letters, 33(12): L12801. doi: 10.1029/2006GL026186 [2] Anderson J L. 2001. An ensemble adjustment Kalman filter for data assimilation. Monthly Weather Review, 129(12): 2884–2903. doi: 10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2 [3] Anderson J L. 2009. Spatially and temporally varying adaptive covariance inflation for ensemble filters. Tellus A, 61(1): 72–83. doi: 10.1111/j.1600-0870.2008.00361.x [4] Annan J D, Hargreaves J C. 2004. Efficient parameter estimation for a highly chaotic system. Tellus A, 56(5): 520–526. doi: 10.3402/tellusa.v56i5.14438 [5] Annan J D, Hargreaves J C, Edwards N R, et al. 2005. Parameter estimation in an intermediate complexity Earth system model using an ensemble Kalman filter. Ocean Modelling, 8(1–2): 135–154 [6] Banks H T. 1992. Computational issues in parameter estimation and feedback control problems for partial differential equation systems. Physica D: Nonlinear Phenomena, 60(1–4): 226–238. [7] Evensen G. 2003. The ensemble Kalman filter: theoretical formulation and practical implementation. Ocean Dynamics, 53(4): 343–367. doi: 10.1007/s10236-003-0036-9 [8] Evensen G, Dee D P, Schröter J. 1998. Parameter estimation in dynamical models. In: Chassignet E P, Verron J, eds. Ocean Modeling and Parameterization. Dordrech, the Netherlands: Springer, 373–398 [9] Ffield A, Gordon A L. 1992. Vertical mixing in the Indonesian thermocline. Journal of Physical Oceanography, 22(2): 184–195. doi: 10.1175/1520-0485(1992)022<0184:VMITIT>2.0.CO;2 [10] Furue R, Jia Yanli, McCreary J P, et al. 2015. Impacts of regional mixing on the temperature structure of the equatorial Pacific Ocean. Part 1: vertically uniform vertical diffusion. Ocean Modelling, 91: 91–111. doi: 10.1016/j.ocemod.2014.10.002 [11] Gaspari G, Cohn S E. 1999. Construction of correlation functions in two and three dimensions. Quarterly Journal of the Royal Meteorological Society, 125(554): 723–757. doi: 10.1002/qj.49712555417 [12] Good S A, Martin M J, Rayner N A. 2013. EN4: quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. Journal of Geophysical Research: Oceans, 118(12): 6704–6716. doi: 10.1002/2013JC009067 [13] Gordon N J, Salmond D J, Smith A F M. 1993. Novel approach to non- linear/non-Gaussian Bayesian state estimation. IEE Proceedings F: Radar and Signal Processing, 140(2): 107–113. doi: 10.1049/ip-f-2.1993.0015 [14] Gregg M C, Sanford T B, Winkel D P. 2003. Reduced mixing from the breaking of internal waves in equatorial waters. Nature, 422(6931): 513–515. doi: 10.1038/nature01507 [15] Jochum M. 2009. Impact of latitudinal variations in vertical diffusivity on climate simulations. Journal of Geophysical Research: Oceans, 114(C1): C01010 [16] Karspeck A R, Danabasoglu G, Anderson J, et al. 2018. A global coupled ensemble data assimilation system using the Community Earth System Model and the Data Assimilation Research Testbed. Quarterly Journal of the Royal Meteorological Society, 144(717): 2404–2430. doi: 10.1002/qj.3308 [17] Kivman G A. 2003. Sequential parameter estimation for stochastic systems. Nonlinear Processes in Geophysics, 10(3): 253–259. doi: 10.5194/npg-10-253-2003 [18] Koyama H, Watanabe M. 2010. Reducing Forecast Errors Due to Model Imperfections Using Ensemble Kalman Filtering. Monthly Weather Review, 138(8): 3316–3332. doi: 10.1175/2010MWR3067.1 [19] Large W G, McWilliams J C, Doney S C. 1994. Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Reviews of Geophysics, 32(4): 363–403. doi: 10.1029/94RG01872 [20] Liu Yun, Liu Zhengyu, Zhang Shaoqing, et al. 2014a. Ensemble-based parameter estimation in a coupled GCM using the adaptive spatial average method. Journal of Climate, 27(11): 4002–4014. doi: 10.1175/JCLI-D-13-00091.1 [21] Liu Yun, Liu Zhengyu, Zhang Shaoqing, et al. 2014b. Ensemble-based parameter estimation in a coupled general circulation model. Journal of Climate, 27(18): 7151–7162. doi: 10.1175/JCLI-D-13-00406.1 [22] Liu J, West M. 2001. Combined parameter and state estimation in simulation-based filtering. In: Sequential Monte Carlo Methods in Practice. New York, NY, USA: Springer, 197–223 [23] Ruiz J J, Pulido M, Miyoshi T. 2013. Estimating model parameters with ensemble-based data assimilation: a review. Journal of the Meteorological Society of Japan, 91(2): 79–99. doi: 10.2151/jmsj.2013-201 [24] Santitissadeekorn N, Jones C. 2015. Two-stage filtering for joint state-parameter estimation. Monthly Weather Review, 143(6): 2028–2042. doi: 10.1175/MWR-D-14-00176.1 [25] Smith R, Jones P W, Briegleb B, et al. 2010. The Parallel Ocean Program (POP) reference manual, ocean component of the community climate system model (CCSM). Technical Report LAUR-10-01853. Boulder, CO, USA: National Centre for Atmosphere Research [26] Tong Mingjing, Xue Ming. 2008. Simultaneous estimation of microphysical parameters and atmospheric state with simulated radar data and ensemble square root Kalman filter. Part I: sensitivity analysis and parameter identifiability. Monthly Weather Review, 136(5): 1630–1648. doi: 10.1175/2007MWR2070.1 [27] Wu Xinrong, Han Guijun, Zhang Shaoqing, et al. 2016. A study of the impact of parameter optimization on ENSO predictability with an intermediate coupled model. Climate Dynamics, 46(3–4): 711–727 [28] Wu Xinrong, Zhang Shaoqing, Liu Zhengyu, et al. 2013. A study of impact of the geographic dependence of observing system on parameter estimation with an intermediate coupled model. Climate Dynamics, 40(7): 1789–1798 [29] Zhang Shaoqing, Liu Zhengyu, Rosati A, et al. 2012. A study of enhancive parameter correction with coupled data assimilation for climate estimation and prediction using a simple coupled model. Tellus A, 64(1): 10963. doi: 10.3402/tellusa.v64i0.10963 [30] Zhang Shaoqing, Liu Zhengyu, Zhang Xuefeng, et al. 2020. Coupled data assimilation and parameter estimation in coupled ocean–atmosphere models: a review. Climate Dynamics, 54(11–12): 5127–5144 [31] Zhang Xuefeng, Zhang Shaoqing, Liu Zhengyu, et al. 2016. Correction of biased climate simulated by biased physics through parameter estimation in an intermediate coupled model. Climate Dynamics, 47(5–6): 1899–1912 [32] Zhao Yuchu, Liu Zhengyu, Zheng Fei, et al. 2019. Parameter optimization for real-world ENSO forecast in an intermediate coupled model. Monthly Weather Review, 147(5): 1429–1445. doi: 10.1175/MWR-D-18-0199.1 [33] Zhu Yuchao, Zhang Ronghua. 2018. An Argo-derived background diffusivity parameterization for improved ocean simulations in the Tropical Pacific. Geophysical Research Letters, 45(3): 1509–1517. doi: 10.1002/2017GL076269 -
下载:
点击查看大图
计量
- 文章访问数: 296
- HTML全文浏览量: 108
- PDF下载量: 16
- 被引次数: 0
