Performance of physical-informed neural network (PINN) for the key parameter inference in Langmuir turbulence parameterization scheme
-
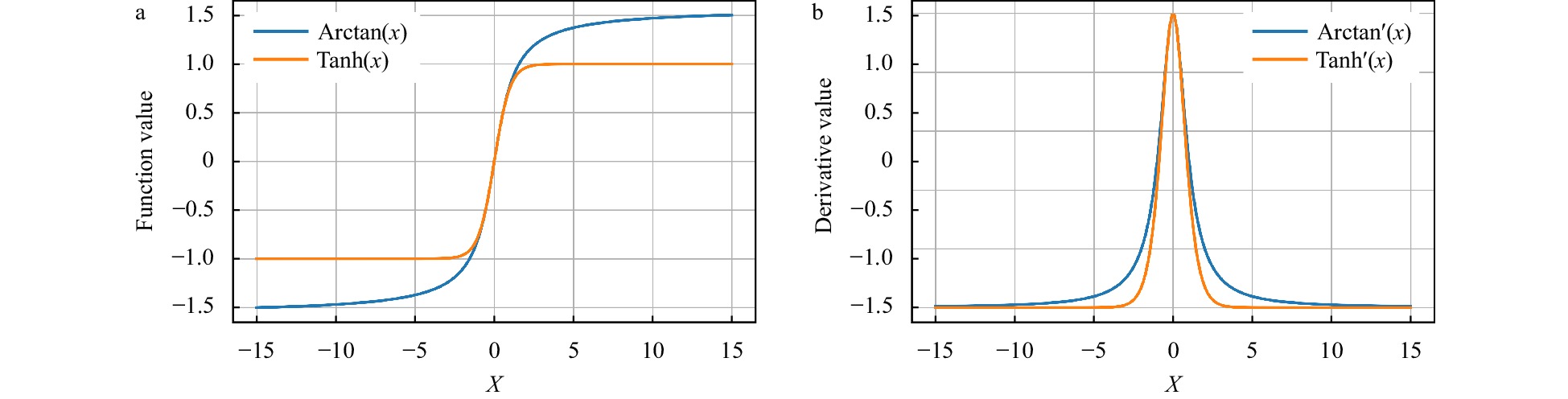
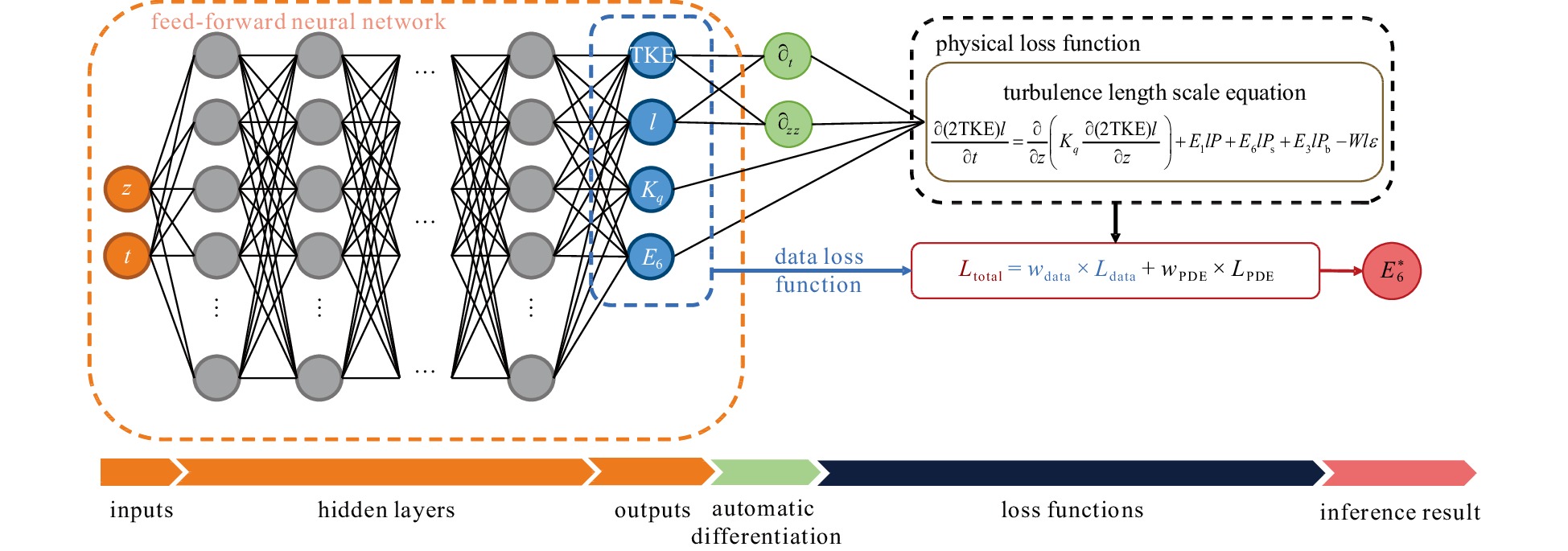
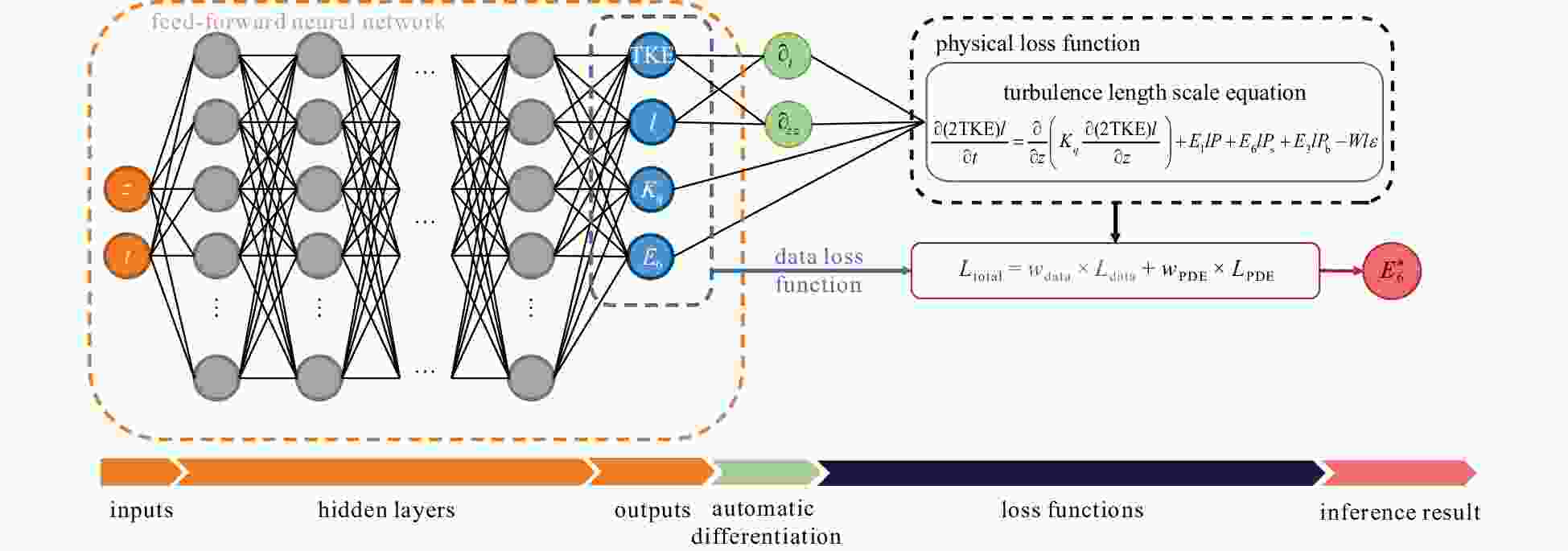
Abstract: The Stokes production coefficient (E6) constitutes a critical parameter within the Mellor-Yamada type (MY-type) Langmuir turbulence (LT) parameterization schemes, significantly affecting the simulation of turbulent kinetic energy, turbulent length scale, and vertical diffusivity coefficient for turbulent kinetic energy in the upper ocean. However, the accurate determination of its value remains a pressing scientific challenge. This study adopted an innovative approach by leveraging deep learning technology to address this challenge of inferring the E6. Through the integration of the information of the turbulent length scale equation into a physical-informed neural network (PINN), we achieved an accurate and physically meaningful inference of E6. Multiple cases were examined to assess the feasibility of PINN in this task, revealing that under optimal settings, the average mean squared error of the E6 inference was only 0.01, attesting to the effectiveness of PINN. The optimal hyperparameter combination was identified using the Tanh activation function, along with a spatiotemporal sampling interval of 1 s and 0.1 m. This resulted in a substantial reduction in the average bias of the E6 inference, ranging from O(101) to O(102) times compared with other combinations. This study underscores the potential application of PINN in intricate marine environments, offering a novel and efficient method for optimizing MY-type LT parameterization schemes.
-
Figure 1. Architecture of physical-informed neural network for key parameter E6 inference in KC04. TKE, turbulent kinetic energy.
Figure 2. Illustration of spatiotemporal sampling interval combinations. a. Illustration for Exp1; b–e. illustration for Exp2.
Figure 4. Inference curves (a–d) and loss curves (e–h) of the E6 inference process in the Exp1.
Figure 5. Average squared errors of E6 inference from all physical-informed neural network models in Set2. Nan indicates that the model gives unstable inferences in all cases.
Figure 6. Results of the temporal group: inference curves (a) and loss curves (b) are the results of Model 2_1; inference curves (c) and loss curves (d) are the results of Model 2_2.
Figure 7. Results of the Spatial group: inference curves (a) and loss curves (b) are the results of Model 2_3; inference curves (c) and loss curves (d) are the results of Model 2_4. The dashed lines of different colors in a represent the preset E6 values in the corresponding cases.
Table 1. Experimental sets and experiment settings
Experimental set (number) Experiment (number) Activation
functionSampling intervals Preset E6 value (case number)/
model numberGOTM sensitivity experiment set (Set1) / / / 5.0 (Case 1), 6.0 (Case 2),
7.0 (Case 3), 8.0 (Case 4)PINN key hyperparameters
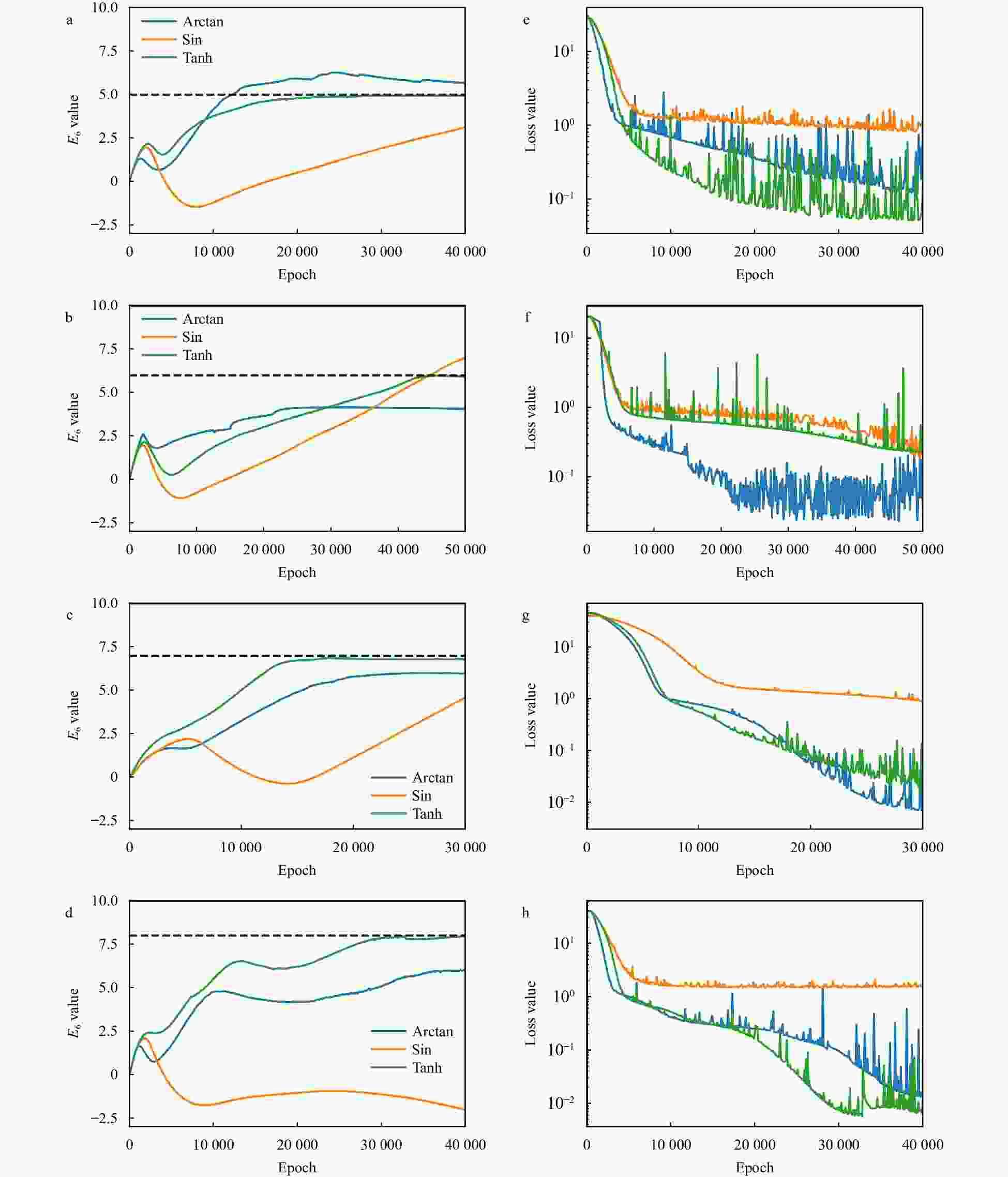
sensitivity experiment set (Set2)Activation Functions sensitivity
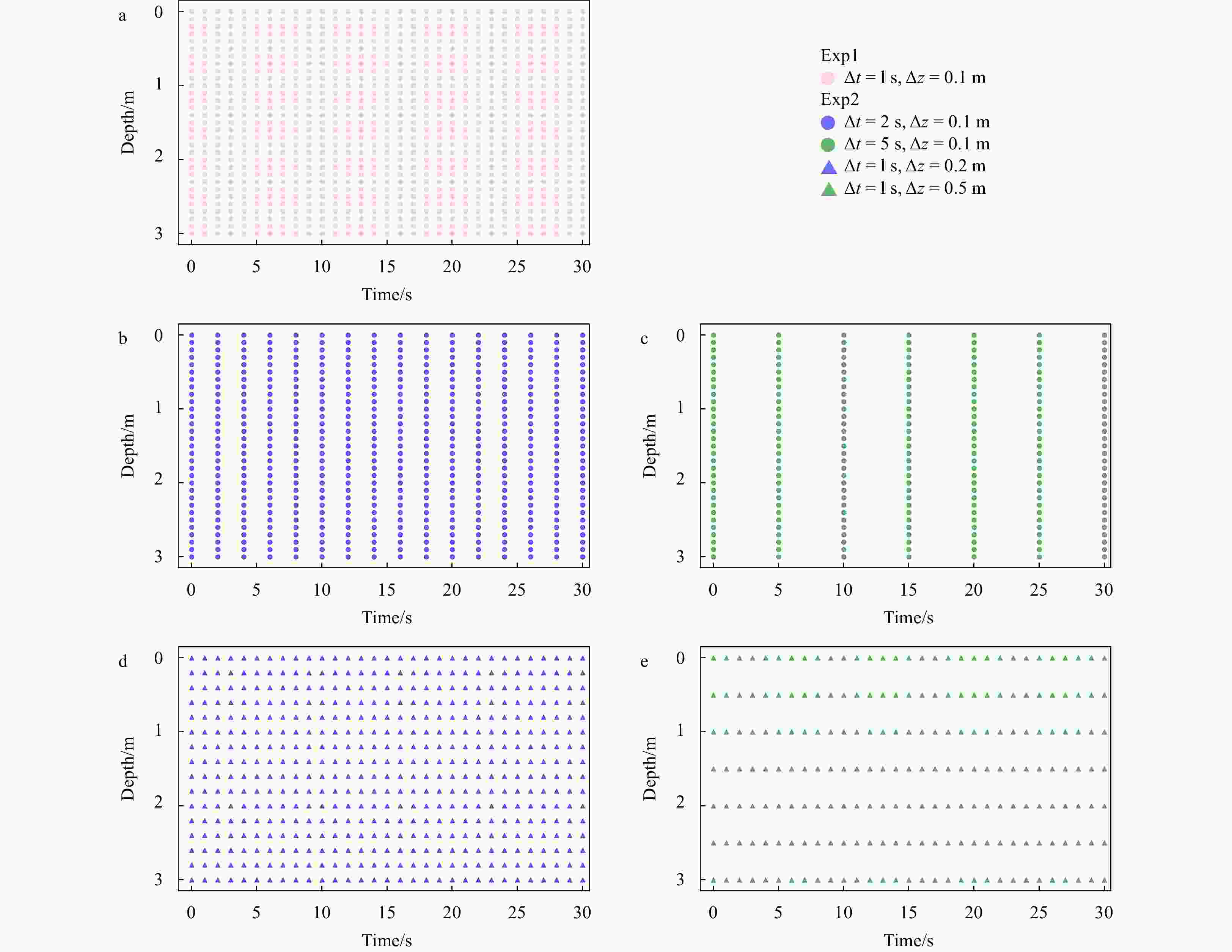
experiment (Exp1)Tanh Δt = 1 s, Δz = 0.1 m Model 1_1 Arctan Δt = 1 s, Δz = 0.1 m Model 1_2 Sin Δt = 1 s, Δz = 0.1 m Model 1_3 Sampling intervals sensitivity
experiment (Exp2)the optimal
one in Exp1Δt = 2 s, Δz = 0.1 m Model 2_1 Δt = 5 s, Δz = 0.1 m Model 2_2 Δt = 1 s, Δz = 0.2 m Model 2_3 Δt = 1 s, Δz = 0.5 m Model 2_4 Notes: / indicates that the item is not set or used in the experiment set. 
下载: 导出CSV
Table 2. Number of sampling points for each PINN model in Set2
Model Spatial number Temporal number Total number Model 1_1, Model 1_2, Model 1_3 300 300 90 000 (300 × 300) Model 2_1 300 150 45 000 (300 × 150) Model 2_2 300 60 18 000 (300 × 60) Model 2_3 150 300 45 000 (150 × 300) Model 2_4 60 300 18 000 (60 × 300)
下载: 导出CSV
Table 3. Inference results and biases of the Exp1
Case Activation function E6 SE Case 1 (E6 = 5.0) Sin / / Arctan / / Tanh 4.903 0 0.0094 Case 2 (E6 = 6.0) Sin / / Arctan 4.062 0 3.7558 Tanh 5.932 0 0.0046 Case 3 (E6 = 7.0) Sin / / Arctan 5.952 0 1.0983 Tanh 6.781 0 0.048 0 Case 4 (E6 = 8.0) Sin / / Arctan 5.999 0 4.004 0 Tanh 7.970 0 0.0009 Note: / indicates that the model fails to reach a stable state in the corresponding case.
下载: 导出CSV
Table 4. Inference results and biases of the temporal group in the Exp2
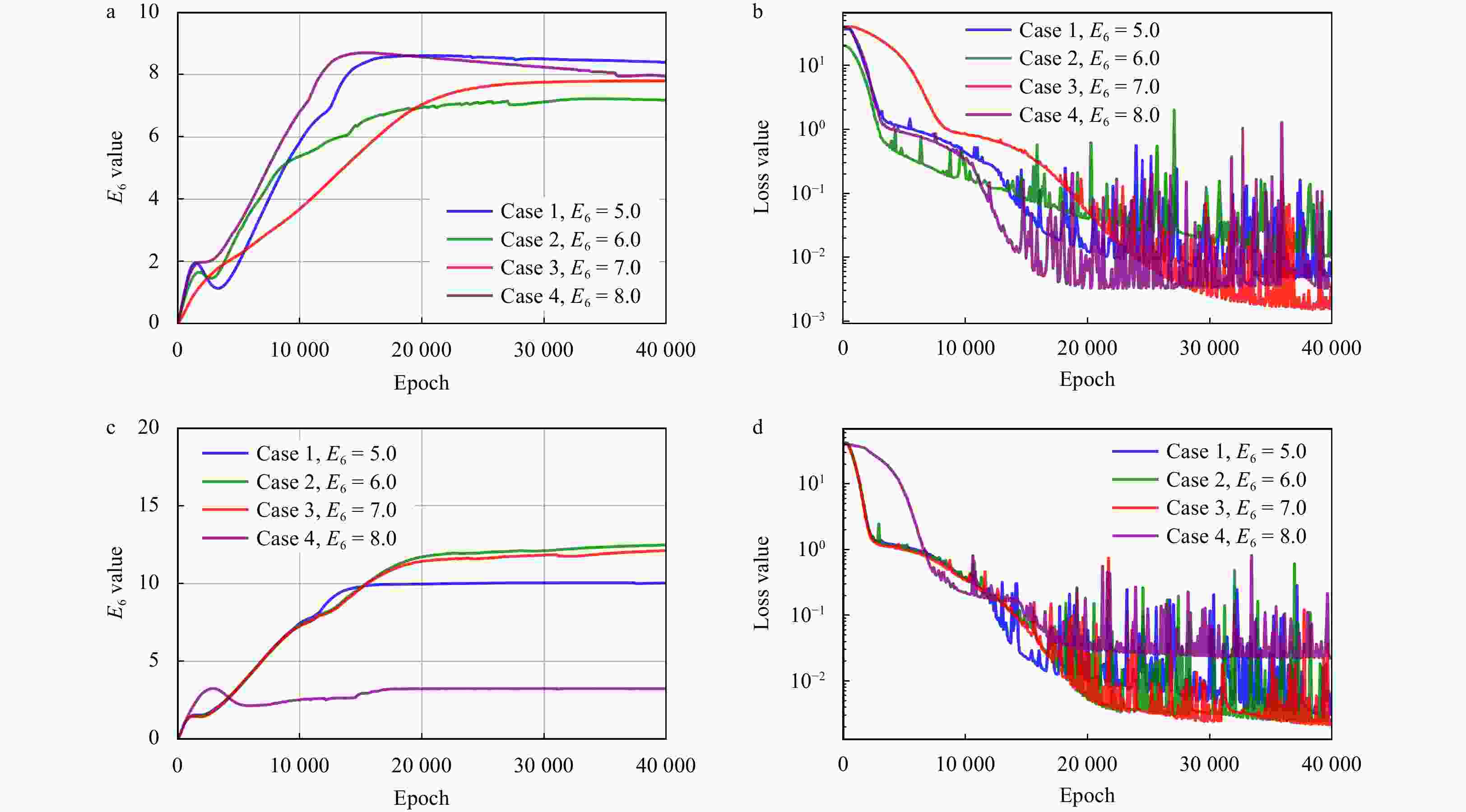
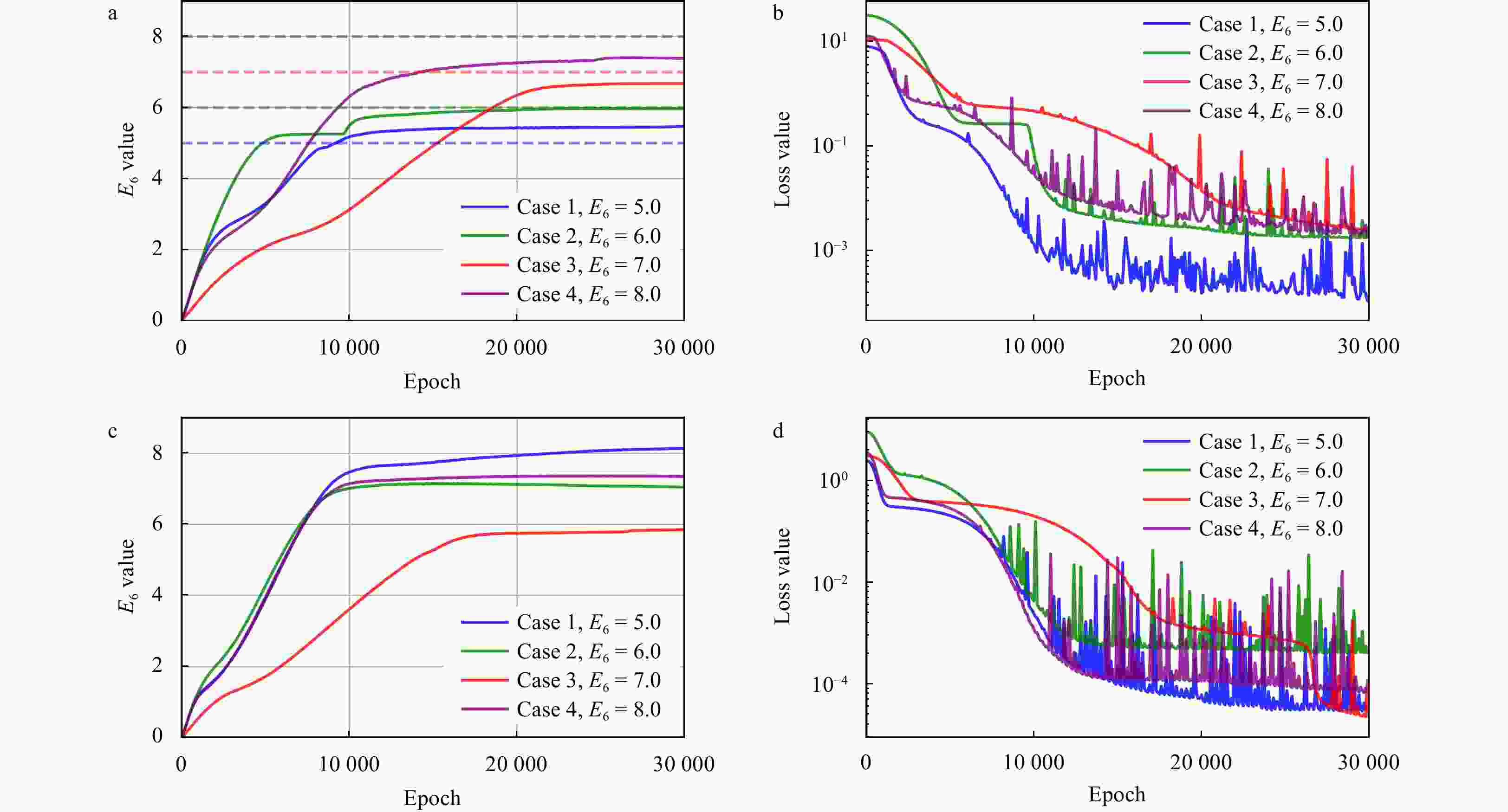
Model Case $ E_6^* $ SE Model 2_1 Case 1 (E6 = 5.0) / / Case 2 (E6 = 6.0) 7.167 1.3619 Case 3 (E6 = 7.0) 7.787 0.6194 Case 4 (E6 = 8.0) / / Model 2_2 Case 1 (E6 = 5.0) 10.027 25.2707 Case 2 (E6 = 6.0) / / Case 3 (E6 = 7.0) / / Case 4 (E6 = 8.0) 3.231 22.7434 Note: / indicates that the PINN model fails to reach a stable state in the corresponding case.
下载: 导出CSV
Table 5. Inference results and biases of the spatial group in the Exp2
Model Case $ E_6^* $ SE Model 2_3 Case 1 (E6 = 5.0) 5.472 0.2228 Case 2 (E6 = 6.0) 5.965 0.0012 Case 3 (E6 = 7.0) 6.675 0.1056 Case 4 (E6 = 8.0) 7.382 0.3819 Model 2_4 Case 1 (E6 = 5.0) / / Case 2 (E6 = 6.0) 7.046 1.0941 Case 3 (E6 = 7.0) 5.846 1.3317 Case 4 (E6 = 8.0) 7.343 0.4316 Note: / indicates that the PINN model fails to reach a stable state in the corresponding case.
下载: 导出CSV
-
Abbasi J, Andersen P Ø. 2023. Physical activation functions (PAFs): an approach for more efficient induction of physics into physics-informed neural networks (PINNs). arXiv: 2205.14630, doi: 10.48550/arXiv.2205.14630 Abdou M A. 2007. The extended tanh method and its applications for solving nonlinear physical models. Applied Mathematics and Computation, 190(1): 988–996, doi: 10.1016/j.amc.2007.01.070 Abueidda D W, Lu Qiyue, Koric S. 2021. Meshless physics-informed deep learning method for three-dimensional solid mechanics. International Journal for Numerical Methods in Engineering, 122(23): 7182–7201, doi: 10.1002/nme.6828 Bajaj C, McLennan L, Andeen T, et al. 2023. Recipes for when physics fails: recovering robust learning of physics informed neural networks. Machine Learning: Science and Technology, 4(1): 015013, doi: 10.1088/2632-2153/acb416 Baydin A G, Pearlmutter B A, Radul A A, et al. 2017. Automatic differentiation in machine learning: a survey. The Journal of Machine Learning Research, 18(1): 5595–5637 Bolandi H, Sreekumar G, Li Xuyang, et al. 2023. Physics informed neural network for dynamic stress prediction. Applied Intelligence, 53(22): 26313–26328, doi: 10.1007/s10489-023-04923-8 Bowman B, Oian C, Kurz J, et al. 2023. Physics-informed neural networks for the heat equation with source term under various boundary conditions. Algorithms, 16(9): 428, doi: 10.3390/a16090428 Cao Yu, Deng Zengan, Wang Chenxu. 2019. Impacts of surface gravity waves on summer ocean dynamics in Bohai Sea. Estuarine, Coastal and Shelf Science, 230: 106443, doi: 10.1016/j.ecss.2019.106443 Cedillo S, Núñez A G, Sánchez-Cordero E, et al. 2022. Physics-informed neural network water surface predictability for 1D steady-state open channel cases with different flow types and complex bed profile shapes. Advanced Modeling and Simulation in Engineering Sciences, 9: 10, doi: 10.1186/s40323-022-00226-8 Craik A D D, Leibovich S. 1976. A rational model for Langmuir circulations. Journal of Fluid Mechanics, 73(3): 401–426, doi: 10.1017/S0022112076001420 Depina I, Jain S, Mar Valsson S, et al. 2022. Application of physics-informed neural networks to inverse problems in unsaturated groundwater flow. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 16(1): 21–36, doi: 10.1080/17499518.2021.1971251 Doronina O A, Murman S M, Hamlington P E. 2020. Parameter estimation for RANS models using approximate bayesian computation. arXiv: 2011.01231, doi: 10.48550/arXiv.2011.01231 Fan Engui. 2000. Extended tanh-function method and its applications to nonlinear equations. Physics Letters A, 277(4/5): 212–218, doi: 10.1016/S0375-9601(00)00725-8 Faroughi S A, Soltanmohammadi R, Datta P, et al. 2024. Physics-informed neural networks with periodic activation functions for solute transport in heterogeneous porous media. Mathematics, 12(1): 63, doi: 10.3390/math12010063 Gimenez J M, Bre F. 2019. Optimization of RANS turbulence models using genetic algorithms to improve the prediction of wind pressure coefficients on low-rise buildings. Journal of Wind Engineering and Industrial Aerodynamics, 193: 103978, doi: 10.1016/j.jweia.2019.103978 Harcourt R R. 2013. A second-moment closure model of langmuir turbulence. Journal of Physical Oceanography, 43(4): 673–697, doi: 10.1175/JPO-D-12-0105.1 Harcourt R R. 2015. An improved second-moment closure model of langmuir turbulence. Journal of Physical Oceanography, 45(1): 84–103, doi: 10.1175/JPO-D-14-0046.1 Hemchandra S, Datta A, Juniper M P. 2023. Learning RANS model parameters from LES using bayesian inference. In: Proceedings of ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition. Boston, USA: ASME, doi: 10.1115/GT2023-102159 Jagtap A D, Kawaguchi K, Karniadakis G E. 2020. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. Journal of Computational Physics, 404: 109136, doi: 10.1016/j.jcp.2019.109136 Kantha L H, Clayson C A. 1994. An improved mixed layer model for geophysical applications. Journal of Geophysical Research: Oceans, 99(C12): 25235–25266, doi: 10.1029/94JC02257 Kantha L H, Clayson C A. 2004. On the effect of surface gravity waves on mixing in the oceanic mixed layer. Ocean Modelling, 6(2): 101–124, doi: 10.1016/S1463-5003(02)00062-8 Kantha L, Lass H U, Prandke H. 2010. A note on Stokes production of turbulence kinetic energy in the oceanic mixed layer: observations in the Baltic Sea. Ocean Dynamics, 60(1): 171–180, doi: 10.1007/s10236-009-0257-7 Kato H, Obayashi S. 2012. Statistical approach for determining parameters of a turbulence model. In: Proceedings of the 2012 15th International Conference on Information Fusion. Singapore: IEEE Krishnapriyan A S, Gholami A, Zhe Shandian, et al. 2021. Characterizing possible failure modes in physics-informed neural networks. In: Proceedings of the 35th Conference on Neural Information Processing Systems. Vancouver, Canada: NeurIPS, 26548–26560 Lederer J. 2021. Activation functions in artificial neural networks: A systematic overview. arXiv: 2101.09957 Lee N, Ajanthan T, Torr P H S, et al. 2021. Understanding the effects of data parallelism and sparsity on neural network training. In: Proceedings of the 9th International Conference on Learning Representations. Washington, DC, USA: ICLR, 11316 Leiteritz R, Pflüger D. 2021. How to avoid trivial solutions in physics-informed neural networks. arXiv: 2112.05620, doi: 10.48550/ARXIV.2112.05620 Li Xuyang, Bolandi H, Salem T, et al. 2022. NeuralSI: structural parameter identification in nonlinear dynamical systems. In: Proceedings of European Conference on Computer Vision. Tel Aviv, Israel: Springer, 332–348 Li Ming, Garrett C, Skyllingstad E. 2005. A regime diagram for classifying turbulent large eddies in the upper ocean. Deep-Sea Research Part I: Oceanographic Research Papers, 52(2): 259–278, doi: 10.1016/j.dsr.2004.09.004 Li Qing, Reichl B G, Fox-Kemper B, et al. 2019. Comparing ocean surface boundary vertical mixing schemes including langmuir turbulence. Journal of Advances in Modeling Earth Systems, 11(11): 3545–3592, doi: 10.1029/2019MS001810 Lou Qin, Meng Xuhui, Karniadakis G E. 2021. Physics-informed neural networks for solving forward and inverse flow problems via the Boltzmann-BGK formulation. Journal of Computational Physics, 447: 110676, doi: 10.1016/j.jcp.2021.110676 Luo Shirui, Vellakal M, Koric S, et al. 2020. Parameter identification of RANS turbulence model using physics-embedded neural network. In: Proceedings of ISC High Performance 2020 International Conference on High Performance Computing. Frankfurt, Germany: Springer, 137–149 Martin P J, Savelyev I B. 2017. Tests of parameterized Langmuir circulation mixing in the ocean’s surface mixed layer II. NRL/MR/7320-17-9738, Naval Research Lab McWilliams J C, Sullivan P P. 2000. Vertical mixing by langmuir circulations. Spill Science & Technology Bulletin, 6(3/4): 225–237, doi: 10.1016/S1353-2561(01)00041-X McWilliams J C, Sullivan P P, Moeng C H. 1997. Langmuir turbulence in the ocean. Journal of Fluid Mechanics, 334: 1–30, doi: 10.1017/S0022112096004375 Mellor G L, Yamada T. 1974. A hierarchy of turbulence closure models for planetary boundary layers. Journal of the Atmospheric Sciences, 31(7): 1791–1806, doi: 10.1175/1520-0469(1974)031<1791:AHOTCM>2.0.CO;2 Mellor G L, Yamada T. 1982. Development of a turbulence closure model for geophysical fluid problems. Reviews of Geophysics, 20(4): 851–875, doi: 10.1029/RG020i004p00851 Moseley B, Markham A, Nissen-Meyer T. 2023. Finite basis physics-informed neural networks (FBPINNs): a scalable domain decomposition approach for solving differential equations. Advances in Computational Mathematics, 49(4): 62, doi: 10.1007/s10444-023-10065-9 Parascandolo G, Huttunen H, Virtanen T. 2017. Taming the waves: sine as activation function in deep neural networks. In: Proceedings of the 5th International Conference on Learning Representations, Washington DC, USA: ICLR Paszke A, Gross S, Chintala S, et al. 2017. Automatic differentiation in PyTorch. In: Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA: NIPS Raissi M, Karniadakis G E. 2018. Hidden physics models: machine learning of nonlinear partial differential equations. Journal of Computational Physics, 357: 125–141, doi: 10.1016/j.jcp.2017.11.039 Raissi M, Perdikaris P, Karniadakis G E. 2019. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378: 686–707, doi: 10.1016/j.jcp.2018.10.045 Ramachandran P, Zoph B, Le Q V. 2018. Searching for activation functions. In: Proceedings of the 6th International Conference on Learning Representations. Vancouver, Canada: OpenReview. net Repp A C, Roberts D M, Slack D J, et al. 1976. A comparison of frequency, interval, and time-sampling methods of data collection. Journal of Applied Behavior Analysis, 9(4): 501–508, doi: 10.1901/jaba.1976.9-501 Sharma R, Shankar V. 2022. Accelerated training of physics-informed neural networks (PINNs) using meshless discretizations. In: Proceedings of the 36th Conference on Neural Information Processing Systems. New Orleans, USA: Curran Associates Inc. , 1034–1046 Sun Jian, Li Xungui, Yang Qiyong, et al. 2023. Hydrodynamic numerical simulations based on residual cooperative neural network. Advances in Water Resources, 180: 104523, doi: 10.1016/j.advwatres.2023.104523 Suzuki N, Fox-Kemper B. 2016. Understanding stokes forces in the wave-averaged equations. Journal of Geophysical Research: Oceans, 121(5): 3579–3596, doi: 10.1002/2015JC011566 Świrszcz G, Czarnecki W M, Pascanu R. 2017. Local minima in training of neural networks. arXiv: 1611.06310 Tartakovsky A M, Marrero C O, Perdikaris P, et al. 2020. Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resources Research, 56(5): e2019WR026731, doi: 10.1029/2019WR026731 Umlauf L, Burchard H. 2005. Second-order turbulence closure models for geophysical boundary layers. a review of recent work. Continental Shelf Research, 25(7/8): 795–827, doi: 10.1016/j.csr.2004.08.004 Umlauf L, Burchard H, Bolding K. 2006. GOTM sourcecode and test case documentation (version 4.0), http://gotm.net/manual/stable/pdf/letter.pdf [2024-01-11] Waheed U B. 2022. Kronecker neural networks overcome spectral bias for PINN-based wavefield computation. IEEE Geoscience and Remote Sensing Letters, 19: 8029805, doi: 10.1109/LGRS.2022.3209901 Wengert R E. 1964. A simple automatic derivative evaluation program. Communications of the ACM, 7(8): 463–464, doi: 10.1145/355586.364791 Wight C L, Zhao Jia. 2020. Solving allen-cahn and cahn-hilliard equations using the adaptive physics informed neural networks. arXiv: 2007.04542 Wu Chenxi, Zhu Min, Tan Qinyang, et al. 2023. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 403: 115671, doi: 10.1016/j.cma.2022.115671 Xiao Heng, Cinnella P. 2018. Quantification of model uncertainty in RANS simulations: a review. Progress in Aerospace Sciences, 108: 1–31, doi: 10.1016/j.paerosci.2018.10.001 Xu Chen, Cao Ba Trung, Yuan Yong, et al. 2023. Transfer learning based physics-informed neural networks for solving inverse problems in engineering structures under different loading scenarios. Computer Methods in Applied Mechanics and Engineering, 405: 115852, doi: 10.1016/j.cma.2022.115852 Yuan Lei, Ni Yiqing, Deng Xiangyun, et al. 2022. A-PINN: auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations. Journal of Computational Physics, 462: 111260, doi: 10.1016/j.jcp.2022.111260 Zhang Xiaoping, Cheng Tao, Ju Lili. 2022. Implicit form neural network for learning scalar hyperbolic conservation laws. In: Proceedings of the 2nd Mathematical and Scientific Machine Learning Conference. Lausanne, Switzerland: PMLR, 1082–1098 Zhang Zhiyong, Zhang Hui, Zhang Lisheng, et al. 2023. Enforcing continuous symmetries in physics-informed neural network for solving forward and inverse problems of partial differential equations. Journal of Computational Physics, 492: 112415, doi: 10.1016/j.jcp.2023.112415 -
点击查看大图
图(8) / 表(5)
计量
- 文章访问数: 93
- HTML全文浏览量: 42
- PDF下载量: 8
- 被引次数: 0
