Cold filament frontogenesis and frontolysis induced by thermal convection turbulence using large eddy simulation
-
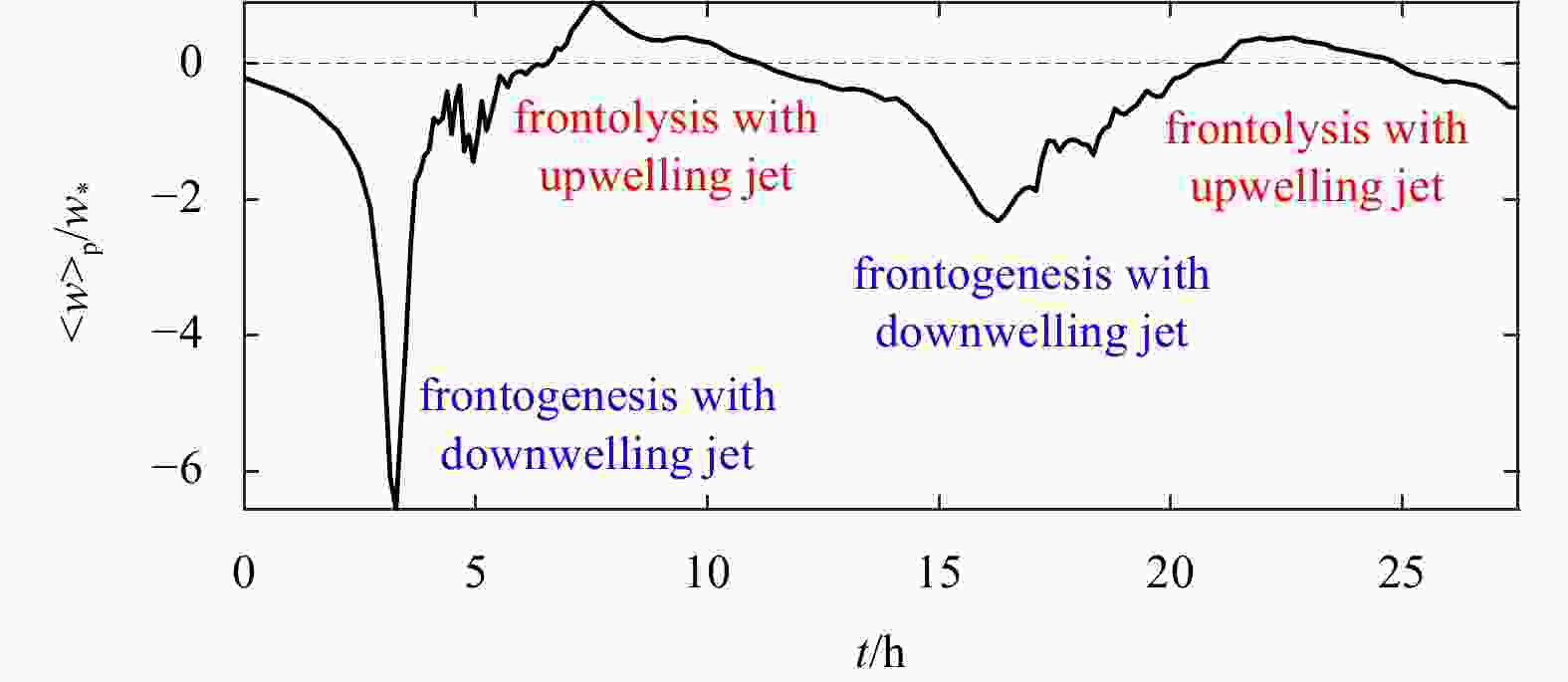
Abstract: The frontogenetic processes of a submesoscale cold filament driven by the thermal convection turbulence are studied by a non-hydrostatic large eddy simulation. The results show that the periodic changes in the direction of the cross-filament secondary circulations are induced by the inertial oscillation. The change in the direction of the secondary circulations induces the enhancement and reduction of the horizontal temperature gradient during the former and later inertial period, which indicates that the frontogenetical processes of the cold filament include both of frontogenesis and frontolysis. The structure of the cold filament may be broken and restored by frontogenesis and frontolysis, respectively. The magnitude of the down-filament currents has a periodic variation, while its direction is unchanged with time. The coupling effect of the turbulent mixing and the frontogenesis and frontolysis gradually weakens the temperature gradient of the cold filament with time, which reduces frontogenetical intensity and enlarges the width of cold filament.
-
Key words:
- cold filament /
- frontogenesis /
- frontolysis /
- thermal convection turbulence /
- large eddy simulation
-
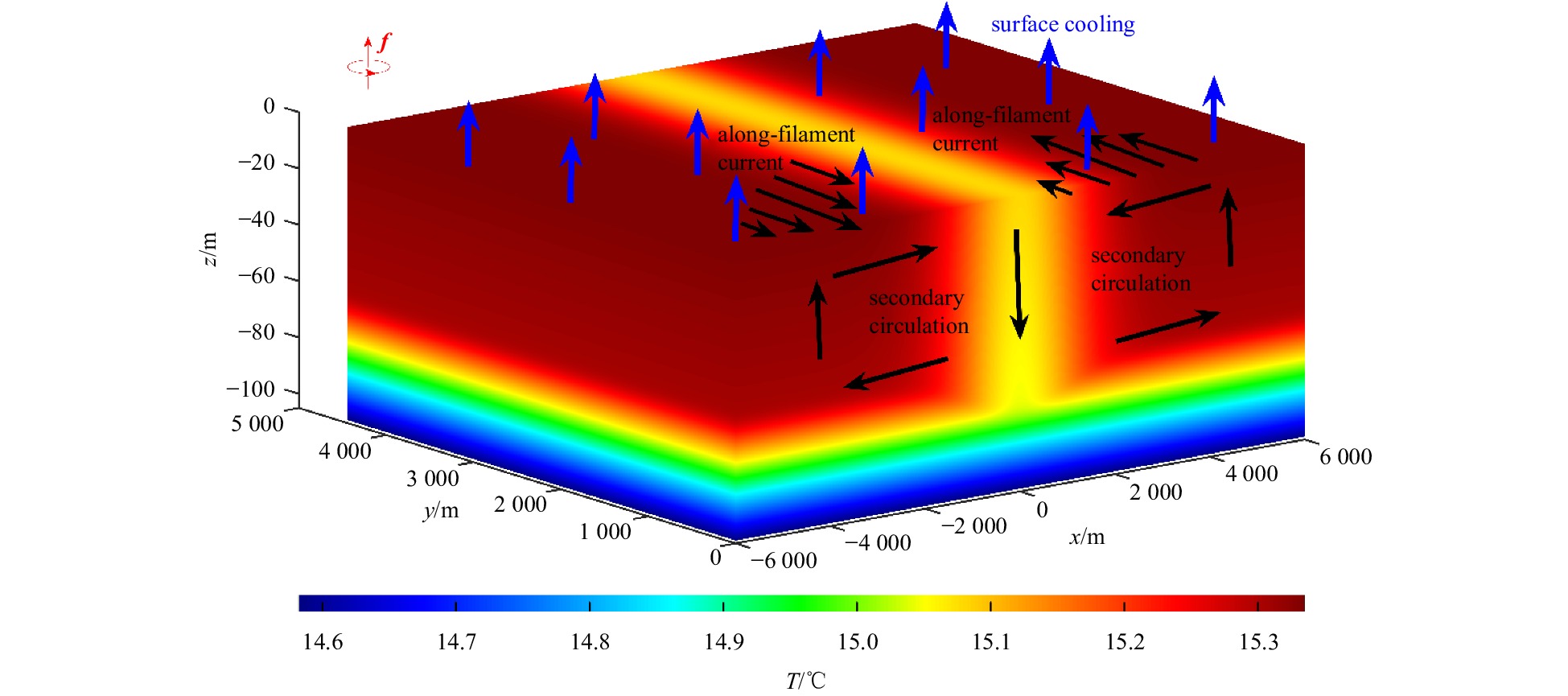
Figure 1. Structures of the submesoscale cold filament, the background submesoscale currents diagnosed by the turbulent thermal wind balance, the surface cooling, and the Coriolis parameter. The black arrow indicates the direction of the submesoscale currents and the blue arrow indicates the direction of sea surface heat flux and the Coriolis parameter (f) is indicated by the red arrow.
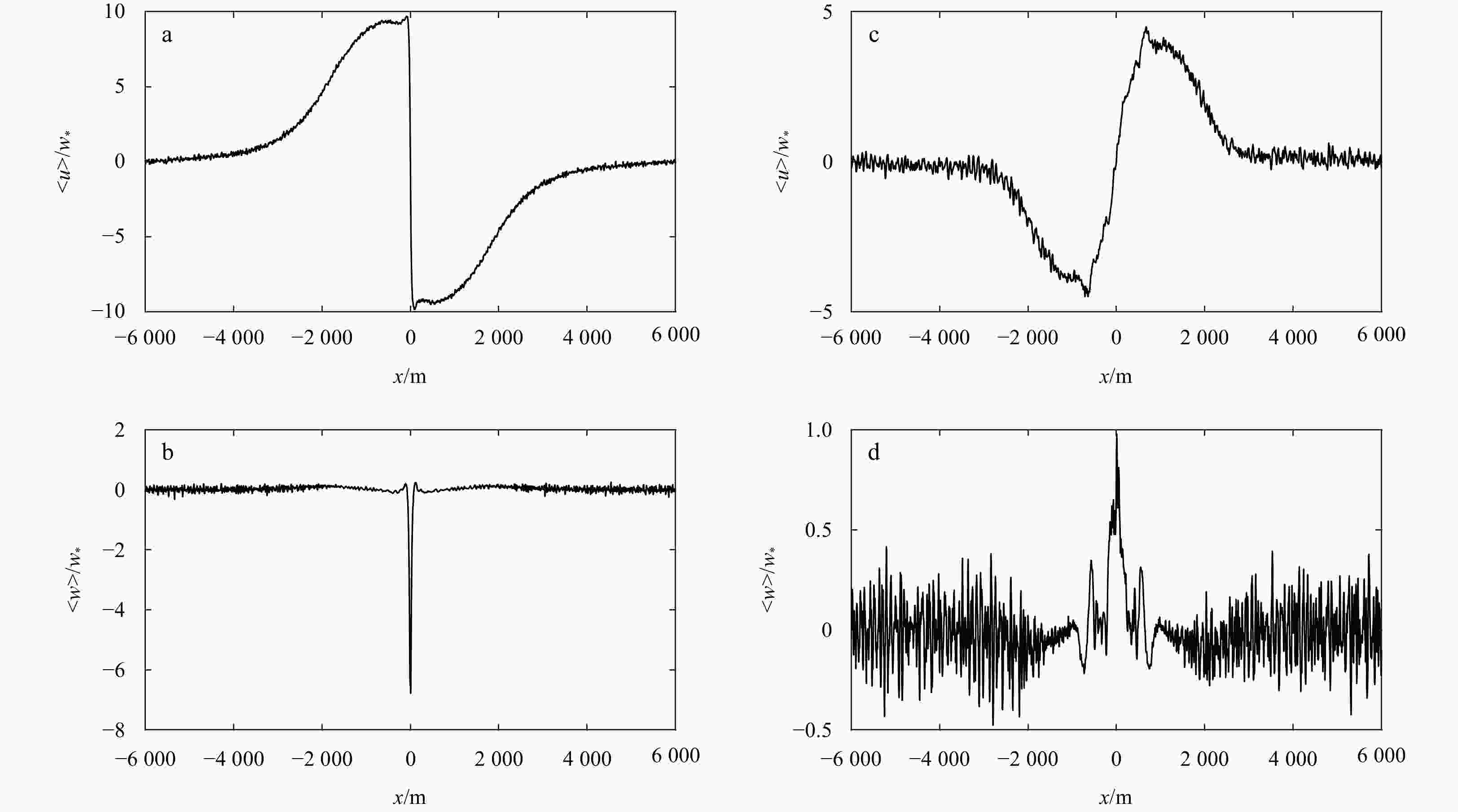
Figure 3. Cross-filament profiles for the normalized cross-filament velocity
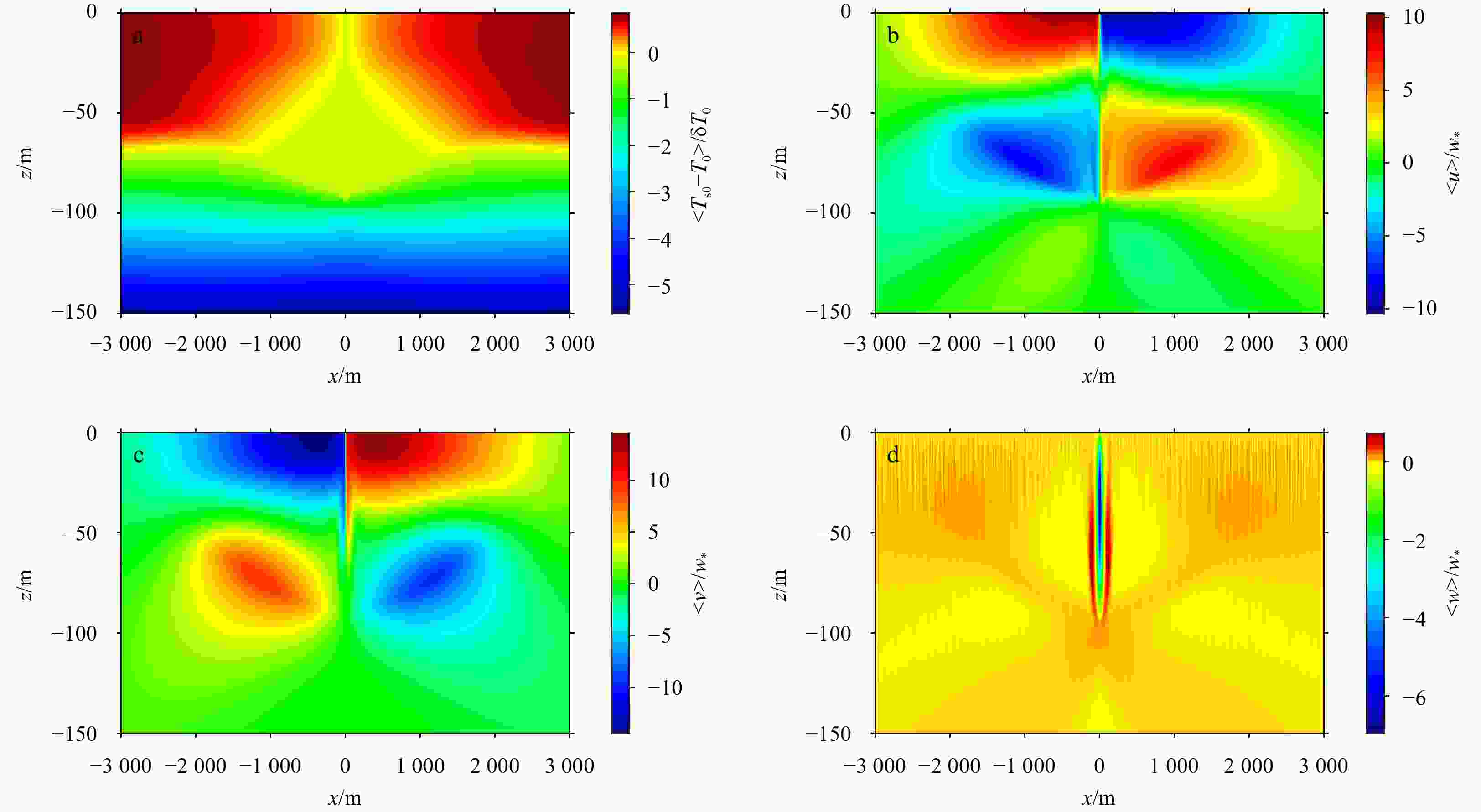
$ \left\langle{u}\right\rangle $ at t = 3.27 h in a near-surface layer of the depth (0 > z > –5 m) (a), the normalized vertical velocity$ \left\langle{w}\right\rangle $ at t = 3.27 h in a middle-layer of the depth (–28 m > z > –32 m) (b), the normalized cross-filament velocity$ \left\langle{u}\right\rangle $ at t = 7.51 h in a near-surface layer of the depth (0 > z > –5 m) (c), and the vertical velocity$ \left\langle{w}\right\rangle $ at t = 7.51 h in a middle-layer of the depth (–28 m > z > –32 m) (d).Figure 4. Average submesoscale flow fields of the normalized temperature
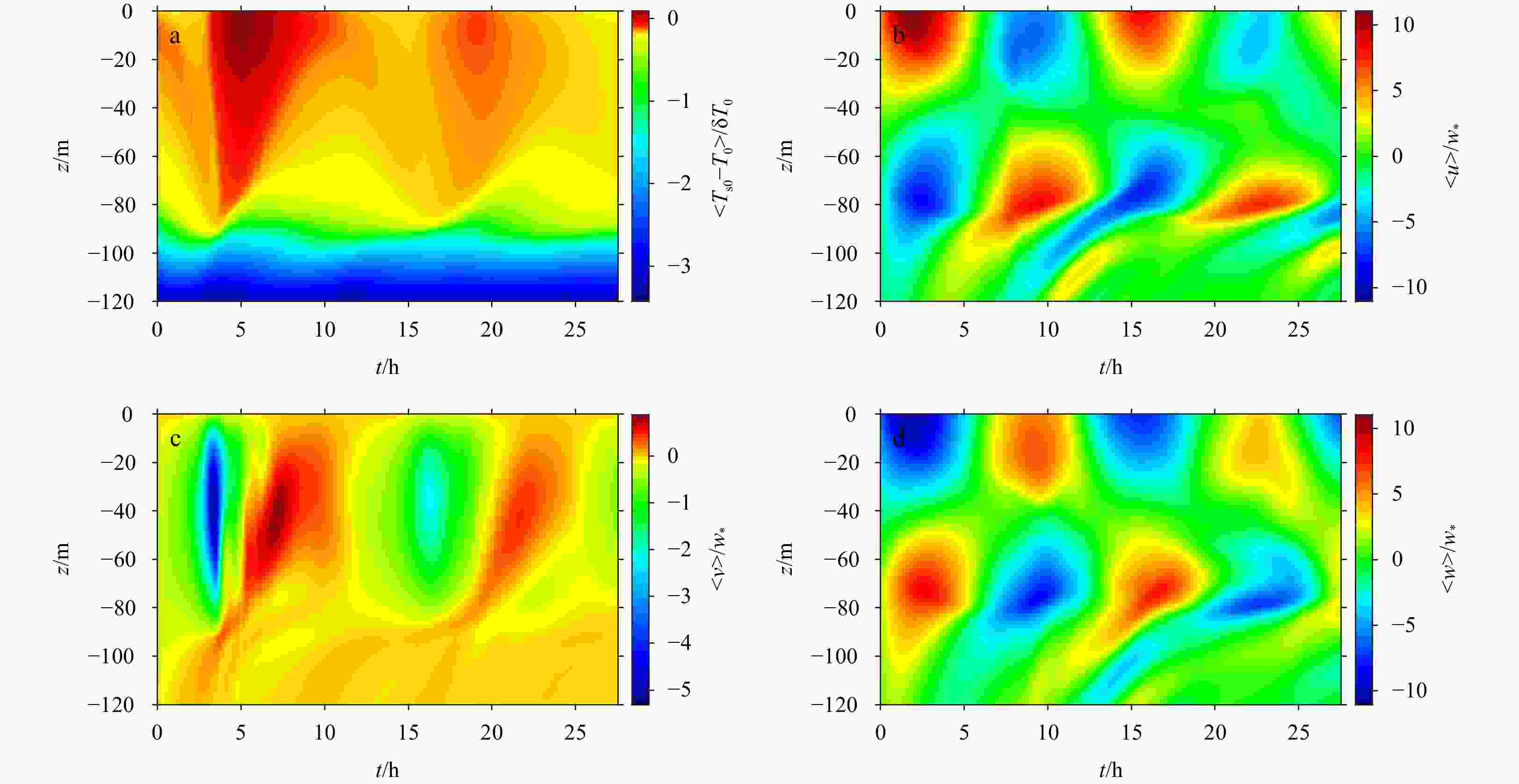
$\left\langle{{T}_{\mathrm{s}0}-{T}_{0}}\right\rangle$ (a), the normalized cross-filament velocity$ \left\langle{u}\right\rangle $ (b), the normalized down-filament velocity$ \left\langle{v}\right\rangle $ (c), and the normalized velocity velocity$ \left\langle{w}\right\rangle $ (d) at t = 3.27 h corresponding to the frontogenesis arrest.Figure 5. Average submesoscale flow fields of the normalized temperature
$\left\langle{{T}_{\mathrm{s}0}-{T}_{0}}\right\rangle\left(\mathrm{a}\right)$ , the normalized cross-filament velocity$ \left\langle{u}\right\rangle\left(\mathrm{b}\right) $ , the normalized down-filament velocity$ \left\langle{v}\right\rangle $ (c), and the normalized velocity velocity$ \left\langle{w}\right\rangle $ (d) at t = 7.51 h corresponding to the frontolysis arrest.Figure 6. The time variation of the submesoscale flow fields in the cross-filament (x) direction for the normalized temperature field
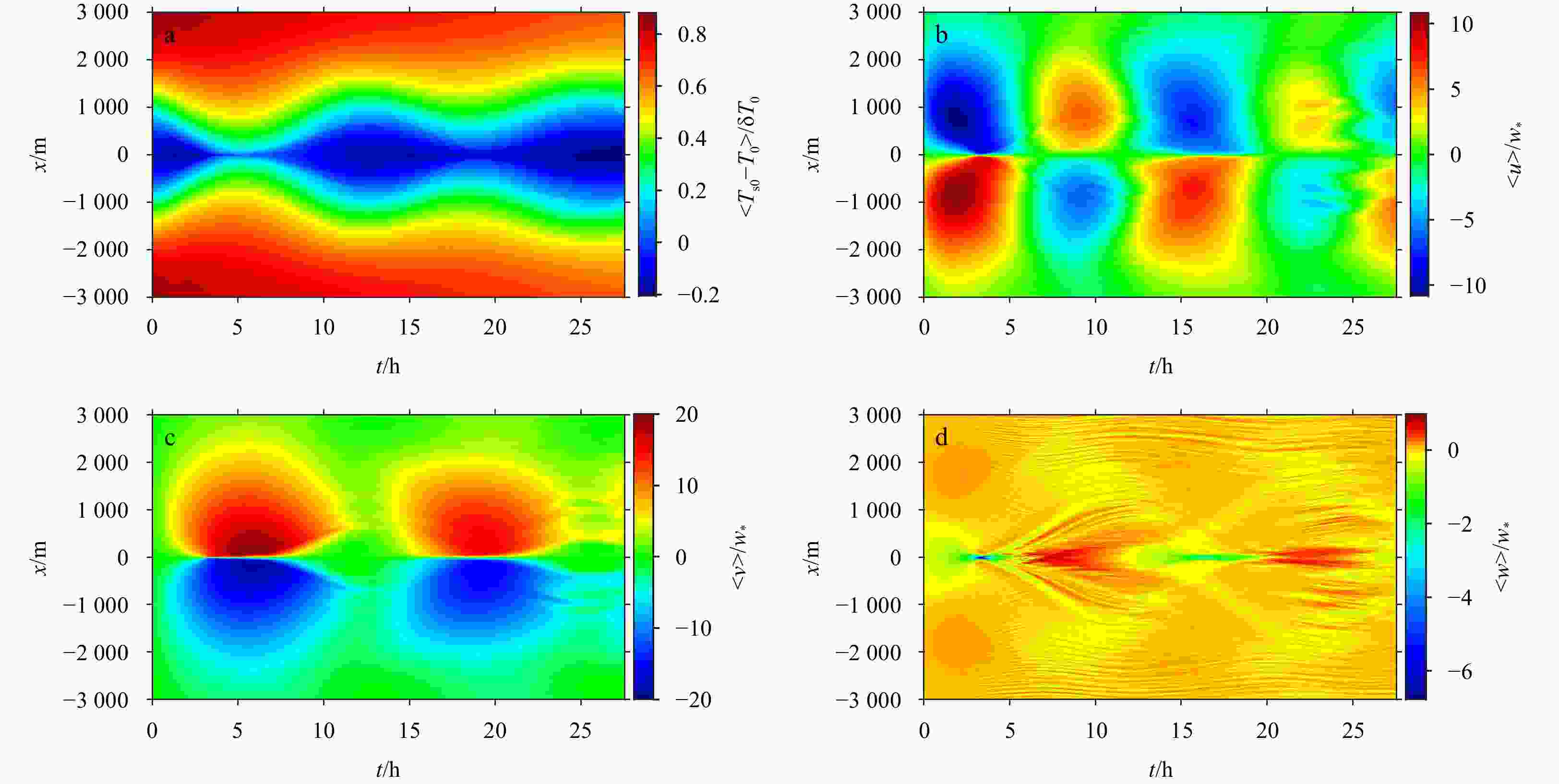
$\left\langle{{T}_{\mathrm{s}0}-{T}_{0}}\right\rangle$ in a near-surface layer (0 m > z > –5 m) (a), the normalized cross-filament current$ \left\langle{u}\right\rangle $ in a near-surface layer (0 m > z > –5 m) (b), the normalized down-filament current$ \left\langle{v}\right\rangle $ in a near-surface layer (0 m > z > –5 m) (c), and the normalized vertical current$ \left\langle{w}\right\rangle $ (d) in the middle of the upper mixed layer (–28 m > z > –32 m).Figure 7. The time variation of the submesoscale flow fields in the vertical (z) direction for the normalized temperature field
$\left\langle{{T}_{\mathrm{s}0}-{T}_{0}}\right\rangle$ at x = 0 that is averaged over –5 m < x < 5 m (a), the normalized cross-filament current$ \left\langle{u}\right\rangle $ at x = –1 000 m that is averaged over –995 m < x < –1 005 m (b), the normalized vertical current$ \left\langle{w}\right\rangle $ in a at x = 0 m that is averaged over –5 m > x > 5 m (c), and the normalized cross-filament current$ \left\langle{u}\right\rangle $ at x = 1 000 m that is averaged over 995 m > x >1005 m (d). -
Barkan R, Molemaker M J, Srinivasan K, et al. 2019. The role of horizontal divergence in submesoscale frontogenesis. Journal of Physical Oceanography, 49(6): 1593–1618, doi: 10.1175/JPO-D-18-0162.1 Blumen W. 2000. Inertial oscillations and frontogenesis in a zero potential vorticity model. Journal of Physical Oceanography, 30(1): 31–39, doi: 10.1175/1520-0485(2000)030<0031:IOAFIA>2.0.CO;2 Bodner A S, Fox-Kemper B, Johnson L, et al. 2023. Modifying the mixed layer eddy parameterization to include frontogenesis arrest by boundary layer turbulence. Journal of Physical Oceanography, 53(1): 323–339, doi: 10.1175/JPO-D-21-0297.1 Bodner A S, Fox-Kemper B, Van Roekel L P, et al. 2020. A perturbation approach to understanding the effects of turbulence on frontogenesis. Journal of Fluid Mechanics, 883: A25 Boccaletti G, Ferrari R, Fox-Kemper B. 2007. Mixed layer instabilities and restratification. Journal of Physical Oceanography, 37(9): 2228–2250, doi: 10.1175/JPO3101.1 Capet X, McWilliams J C, Molemaker M J, et al. 2008a. Mesoscale to submesoscale transition in the California current system. Part I: Flow structure, eddy flux, and observational tests. Journal of Physical Oceanography, 38(1): 29–43, doi: 10.1175/2007 JPO3671.1 Capet X, McWilliams J C, Molemaker M J, et al. 2008b. Mesoscale to submesoscale transition in the California current system. Part II: Frontal processes. Journal of Physical Oceanography, 38(1): 44–64, doi: 10.1175/2007JPO3672.1 Capet X, McWilliams J C, Molemaker M J, et al. 2008c. Mesoscale to submesoscale transition in the California current system. Part III: Energy balance and flux. Journal of Physical Oceanography, 38(10): 2256–2268, doi: 10.1175/2008JPO3810.1 Crowe M N, Taylor J R. 2018. The evolution of a front in turbulent thermal wind balance. Part 1. Theory. Journal of Fluid Mechanics, 850: 179–211, doi: 10.1017/jfm.2018.448 Crowe M N, Taylor J R. 2019. The evolution of a front in turbulent thermal wind balance. Part 2. Numerical simulations. Journal of Fluid Mechanics, 880: 326–352, doi: 10.1017/jfm.2019.688 Dauhajre D P, McWilliams J C, Uchiyama Y. 2017. Submesoscale coherent structures on the continental shelf. Journal of Physical Oceanography, 47(12): 2949–2976, doi: 10.1175/JPO-D-16-0270.1 Deardorff J W. 1972. Numerical investigation of neutral and unstable planetary boundary layers. Journal of the Atmospheric Sciences, 29(1): 91–115, doi: 10.1175/1520-0469(1972)029<0091:NIONAU>2.0.CO;2 Fox-Kemper B, Ferrari R, Hallberg R. 2008. Parameterization of mixed layer eddies. Part I: Theory and diagnosis. Journal of Physical Oceanography, 38(6): 1145–1165, doi: 10.1175/2007JPO3792.1 Gula J T, Molemaker M J, McWilliams J C. 2014. Submesoscale cold filaments in the Gulf Stream. Journal of Physical Oceanography, 44(10): 2617–2643, doi: 10.1175/JPO-D-14-0029.1 Hamlington P E, Van Roekel L P, Fox-Kemper B, et al. 2014. Langmuir-submesoscale interactions: Descriptive analysis of multiscale frontal spindown simulations. Journal of Physical Oceanography, 44(9): 2249–2272, doi: 10.1175/JPO-D-13-0139.1 Haney S, Fox-Kemper B, Julien K, et al. 2015. Symmetric and geostrophic instabilities in the wave-forced ocean mixed layer. Journal of Physical Oceanography, 45(12): 3033–3056, doi: 10.1175/JPO-D-15-0044.1 Hoskins B J. 1982. The mathematical theory of frontogenesis. Annual Review of Fluid Mechanics, 14: 131–151, doi: 10.1146/annurev.fl.14.010182.001023 Hypolite D, Romero L, McWilliams J C, et al. 2021. Surface gravity wave effects on submesoscale currents in the open ocean. Journal of Physical Oceanography, 51(11): 3365–3383 Kaminski A K, Smyth W D. 2019. Stratified shear instability in a field of pre-existing turbulence. Journal of Fluid Mechanics, 862: 639–658, doi: 10.1017/jfm.2018.973 Lapeyre G, Klein P, Hua B L. 2006. Oceanic restratification forced by surface frontogenesis. Journal of Physical Oceanography, 36(8): 1577–1590, doi: 10.1175/JPO2923.1 Leibovich S. 1983. The form and dynamics of Langmuir circulations. Annual Review of Fluid Mechanics, 15: 391–427, doi: 10.1146/annurev.fl.15.010183.002135 Li Guojing, Wang Dongxiao, Dong Changming, et al. 2024. Frontogenesis and frontolysis of a cold filament driven by the cross-filament wind and wave fields simulated by a large eddy simulation. Advances in Atmospheric Sciences, 41(3): 509–528, doi: 10.1007/s00376-023-3037-2 McWilliams J C. 2016. Submesoscale currents in the ocean. Proceedings of the Royal Society A: Mathematical, Physical, and Engineering Sciences, 472(2189): 20160117 McWilliams J C. 2017. Submesoscale surface fronts and filaments: secondary circulation, buoyancy flux, and frontogenesis. Journal of Fluid Mechanics, 823: 391–432, doi: 10.1017/jfm.2017.294 McWilliams J C. 2018. Surface wave effects on submesoscale fronts and filaments. Journal of Fluid Mechanics, 843: 479–517, doi: 10.1017/jfm.2018.158 McWilliams J C. 2019. A survey of submesoscale currents. Geoscience Letters, 6(1): 3, doi: 10.1186/s40562-019-0133-3 McWilliams J C. 2021. Oceanic frontogenesis. Annual Review of Marine Science, 13: 227–253, doi: 10.1146/annurev-marine-032320-120725 McWilliams J C, Colas F, Molemaker M J. 2009. Cold filamentary intensification and oceanic surface convergence lines. Geophysical Research Letters, 36(18): L18602, doi: 10.1029/2009GL039402 McWilliams J C, Fox-Kemper B. 2013. Oceanic wave-balanced surface fronts and filaments. Journal of Fluid Mechanics, 730: 464–490, doi: 10.1017/jfm.2013.348 McWilliams J C, Gula J, Molemaker M J, et al. 2015. Filament frontogenesis by boundary layer turbulence. Journal of Physical Oceanography, 45(8): 1988–2005, doi: 10.1175/JPO-D-14-0211.1 McWilliams J C, Sullivan P P, Moeng C H. 1997. Langmuir turbulence in the ocean. Journal of Fluid Mechanics, 334: 1–30, doi: 10.1017/S0022112096004375 Moeng C H. 1984. A large-eddy-simulation model for the study of planetary boundary-layer turbulence. Journal of the Atmospheric Sciences, 46(13): 2052–2062 Pham H T, Sarkar S. 2018. Ageostrophic secondary circulation at a submesoscale front and the formation of gravity currents. Journal of Physical Oceanography, 48(10): 2507–2529, doi: 10.1175/JPO-D-17-0271.1 Shakespeare C J, Taylor J R. 2013. A generalized mathematical model of geostrophic adjustment and frontogenesis: Uniform potential vorticity. Journal of Fluid Mechanics, 736: 366–413, doi: 10.1017/jfm.2013.526 Skyllingstad E D, Denbo D W. 1995. An ocean large-eddy simulation of Langmuir circulations and convection in the surface mixed layer. Journal of Geophysical Research: Oceans, 100(C5): 8501–8522, doi: 10.1029/94JC03202 Skyllingstad E D, Samelson R M. 2012. Baroclinic frontal instabilities and turbulent mixing in the surface boundary layer. Part I: Unforced simulations. Journal of Physical Oceanography, 42(10): 1701–1716, doi: 10.1175/JPO-D-10-05016.1 Smith K M, Hamlington P E, Fox-Kemmper B. 2016. Effects of submesoscale turbulence on ocean tracers. Journal of Geophysical Research: Oceans, 121(1): 908–933, doi: 10.1002/2015JC011089 Sullivan P P, McWilliams J C. 2018. Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer. Journal of Fluid Mechanics, 837: 341–380, doi: 10.1017/jfm.2017.833 Sullivan P P, McWilliams J C. 2019. Langmuir turbulence and filament frontogenesis in the oceanic surface boundary layer. Journal of Fluid Mechanics, 879: 512–553, doi: 10.1017/jfm.2019.655 Sullivan P P, McWilliams J C. 2024. Oceanic frontal turbulence. Journal of Physical Oceanography, 54(2): 333–358, doi: 10.1175/JPO-D-23-0033.1 Sullivan P P, McWilliams J C, Melville W K. 2007. Surface gravity wave effects in the oceanic boundary layer: Large-eddy simulation with vortex force and stochastic breakers. Journal of Fluid Mechanics, 593: 405–452, doi: 10.1017/S002211200700897X Sullivan P P, McWilliams J C, Moeng C H. 1994. A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorology, 71(3): 247–276, doi: 10.1007/BF00713741 Sullivan P P, Patton E G. 2011. The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. Journal of the Atmospheric Sciences, 68(10): 2395–2413, doi: 10.1175/JAS-D-10-05010.1 Suzuki N, Fox-Kemper B. 2016. Understanding stokes forces in the wave-averaged equations. Journal of Geophysical Research: Oceans, 121(5): 3579–3596, doi: 10.1002/2015JC011566 Taylor J R, Thompson A F. 2023. Submesoscale dynamics in the upper ocean. Annual Review of Fluid Mechanics, 55: 103–127, doi: 10.1146/annurev-fluid-031422-095147 Verma V, Pham H T, Sarkar S. 2019. The submesoscale, the finescale and their interaction at a mixed layer front. Ocean Modelling, 140: 101400, doi: 10.1016/j.ocemod.2019.05.004 Yuan Jianguo, Liang Junhong. 2021. Wind-and wave-driven ocean surface boundary layer in a frontal zone: Roles of submesoscale eddies and Ekman-Stokes transport. Journal of Physical Oceanography, 51(8): 2655–2680 Wang Dailin. 2011. Large-eddy simulation of the diurnal cycle of oceanic boundary layer: sensitivity to domain size and spatial resolution. Journal of Geophysical Research: Oceans, 106(C7): 13959–13974 Zhang Zhiwei, Liu Yuelin, Qiu Bo, et al. 2023a. Submesoscale inverse energy cascade enhances Southern Ocean eddy heat transport. Nature Communications, 14(1): 1335, doi: 10.1038/s41467-023-36991-2 Zhang Zhiwei, Zhang Xincheng, Qiu Bo, et al. 2021. Submesoscale currents in the subtropical upper ocean observed by long-term high-resolution mooring arrays. Journal of Physical Oceanography, 51(1): 187–206, doi: 10.1175/JPO-D-20-0100.1 Zhang Jinchao, Zhang Zhiwei, Qiu Bo. 2023b. Parameterizing submesoscale vertical buoyancy flux by simultaneously considering baroclinic instability and strain-induced frontogenesis. Geophysical Research Letters, 50(8): e2022GL102292, doi: 10.1029/2022GL102292 -




 下载:
下载: