-
Abstract: We introduce a new method, the piecewise Reynolds mean (PREM), for decomposing the flow velocity into the mean-flow and eddy-flow parts in the time domain for subsequent calculation of the mean flow kinetic energy (MKE) and eddy kinetic energy (EKE). Compared with conventional methods like the Reynolds mean and running mean (RUM), PREM has the advantage of exact balance between the MKE and EKE, without the additional residual kinetic energy (RKE), while retaining time-dependent mean-flow. It is mathematically simple and computationally lightweight, depending on a pre-defined separation scale for the mean-flow and eddies. Based on satellite observations and the separation scale of 1 year, we compare PREM with RUM, as well as another newly proposed method, the eddy detection and extraction (EDEX). The latter is based on objective identification of mesoscale eddies and eddy anomaly extraction algorithms, and is therefore only suitable for mesoscale eddy energetics, but independent of separation scales. It is shown that compared with RUM, PREM gives larger mean EKE and stronger interannual variability. In strong-current and eddy-rich regions, the two methods differ the most (max: Kuroshio Extension, root-mean-sqaure-difference = 60.3 J/m3); but in areas with weak current and eddy, the difference accounts for the largest fraction of total EKE (max: south of the Aleutian Islands, 208%). EKE estimated by the two methods is out of phase (min correlation coefficient = 0.38). The mean EKE and standard deviation from the EDEX method resemble the PREM with 1-year separation scale, but is generally smaller in magnitude.
-
Key words:
- mesoscale eddy /
- kinetic energy /
- piecewise Reynolds mean
-
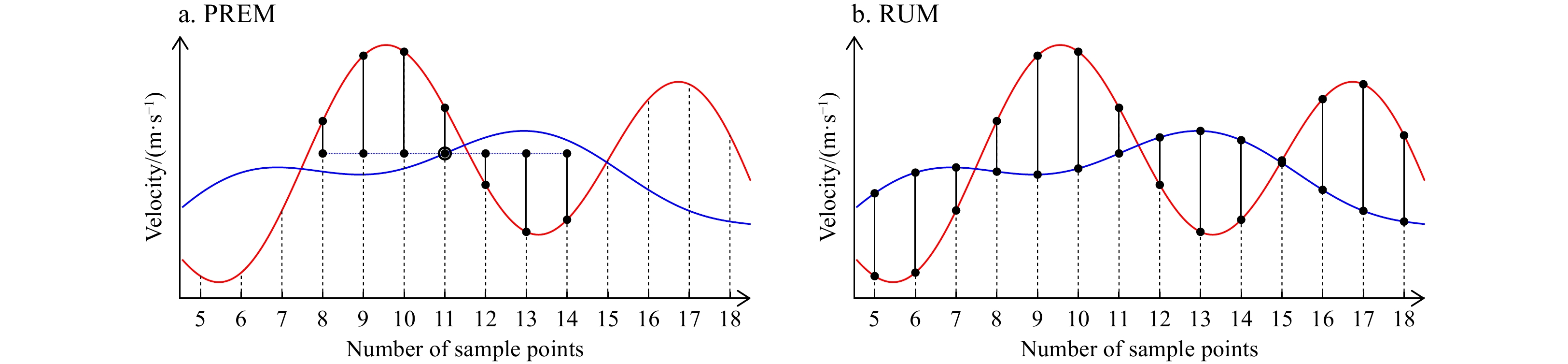
Figure 1. Schematic diagram of the PREM (a) and RUM (b) methods. Red curves are the original time series of velocity, and blue curves are the running-averaged velocity. Black bars with dots denote the perturbation velocity (difference between original and running-average) used for calculating the EKE within each window (in RUM the window size is unity).
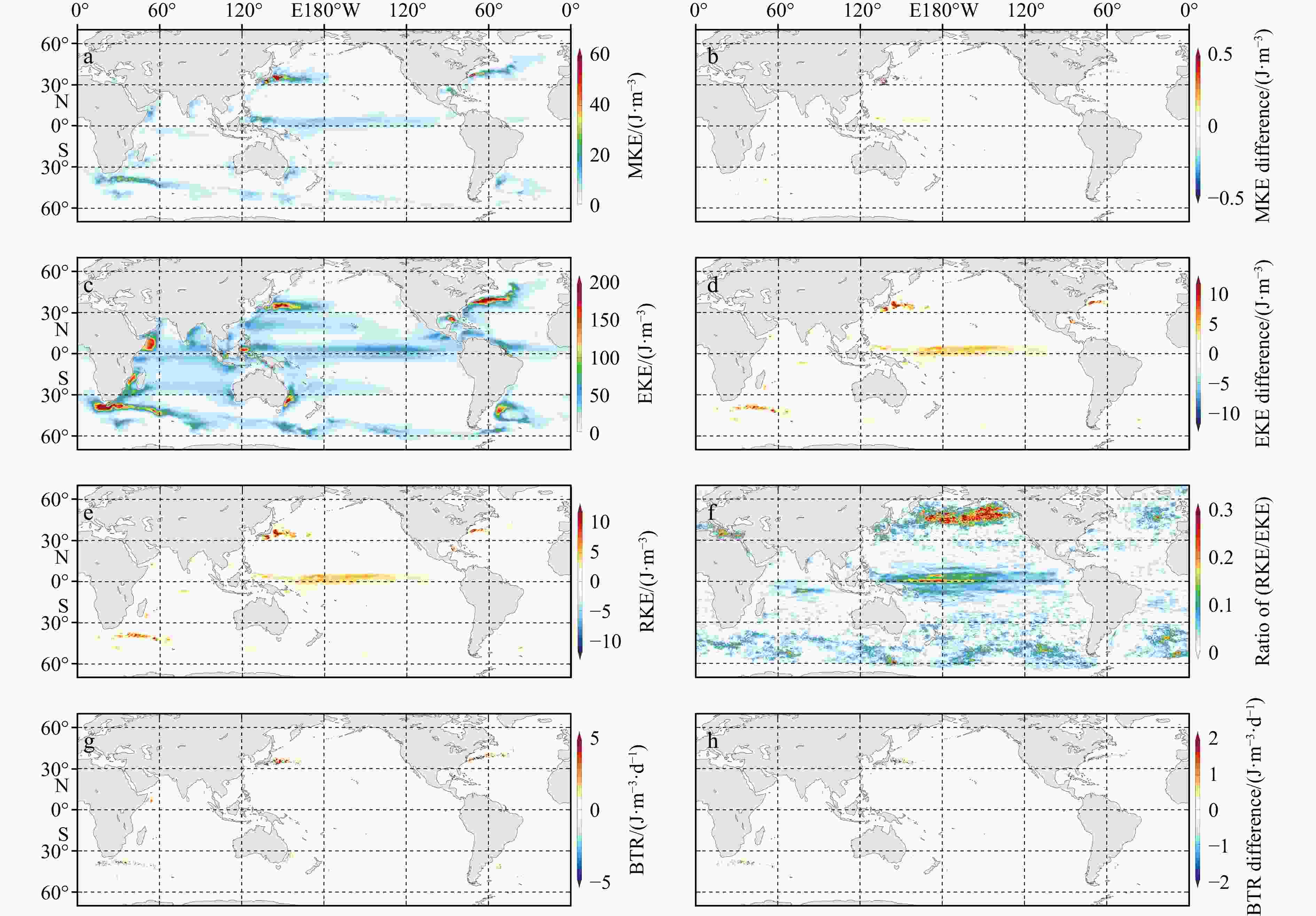
Figure 2. Comparison of 28-year averaged energy terms and conversion rate estimated by the PREM and RUM methods. a. MKE of the PREM method; b. MKE difference of PREM-RUM; c. EKE of the PREM method; d. EKE difference of PREM-RUM; e. RKE of the RUM method; f. ratio of RKE/EKE of the RUM method; g. BTR of the PREM method; h. BTR difference of PREM-RUM.
Figure 3. Comparison of interannual standard deviation (STD) of energy terms and conversion rate estimated by the PREM and RUM methods. a. MKE of the PREM method; b. MKE difference of PREM-RUM; c. EKE of the PREM method; d. EKE difference of PREM-RUM; e. RKE of the RUM method; f. ratio of RKE/EKE of the RUM method; g. BTR of the PREM method; h. BTR difference of PREM-RUM.
Figure 4. Root-mean-square (RMS) difference between the energy terms and conversion rate estimated by the PREM and RUM methods. Left column, a, c and e. RMS difference; right column, b, d, and f. RMS difference divided by standard deviation of the energy term estimated by the RUM method. The energy terms are MKE (top row, a and b), EKE (middle row, c and d), and BTR (bottom row, e and f).
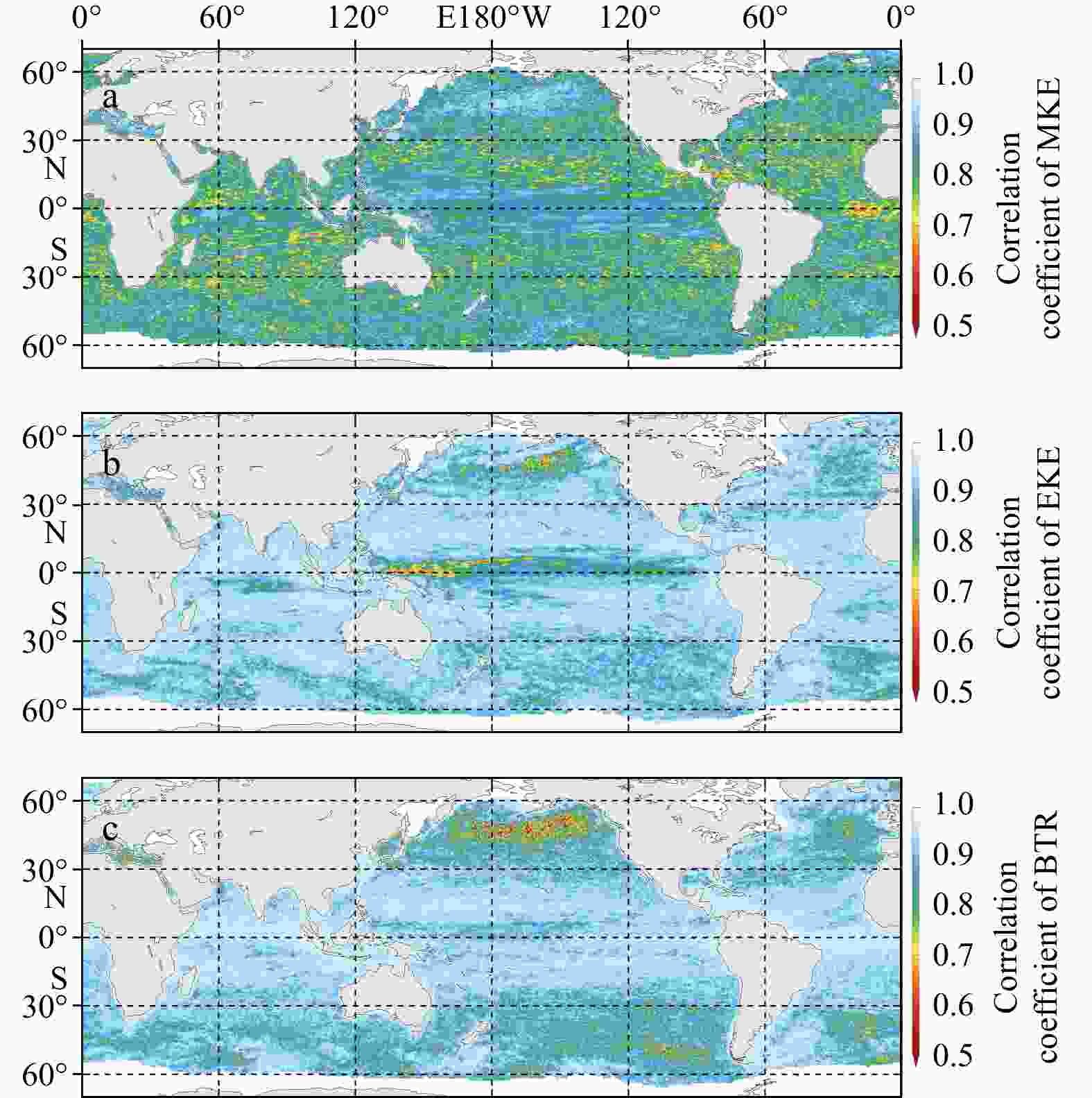
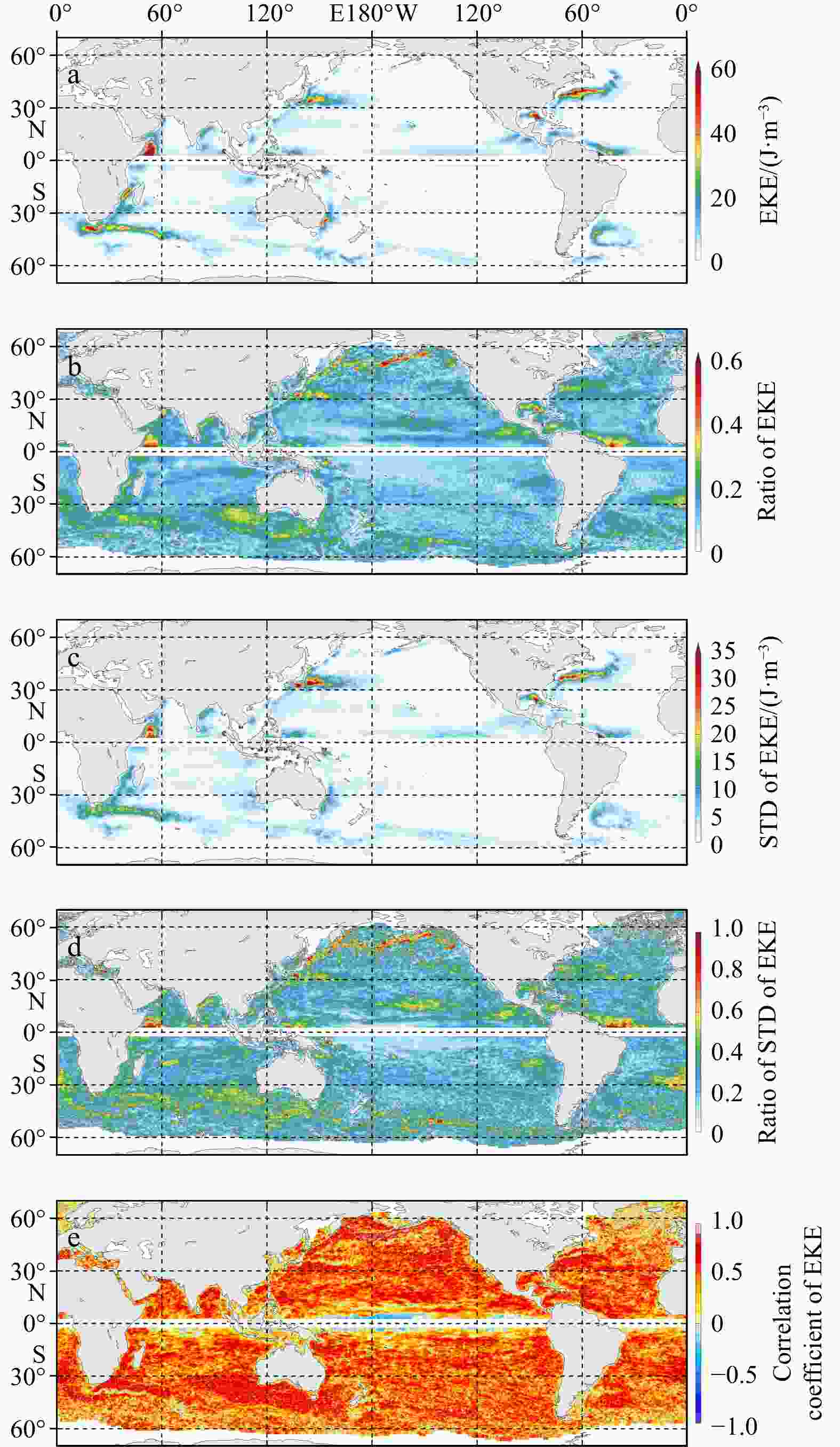
Figure 6. 28-year averaged EKE (J/m3) estimated by the EDEX method (a), fraction of 28-year averaged EKE of the EDEX method relative to the PREM method (b), interannual standard deviation of EKE of the EDEX method (c), fraction of interannual standard deviation of the EDEX method relative to the PREM method (d), and correlation of EKE of the EDEX and PREM methods (e).
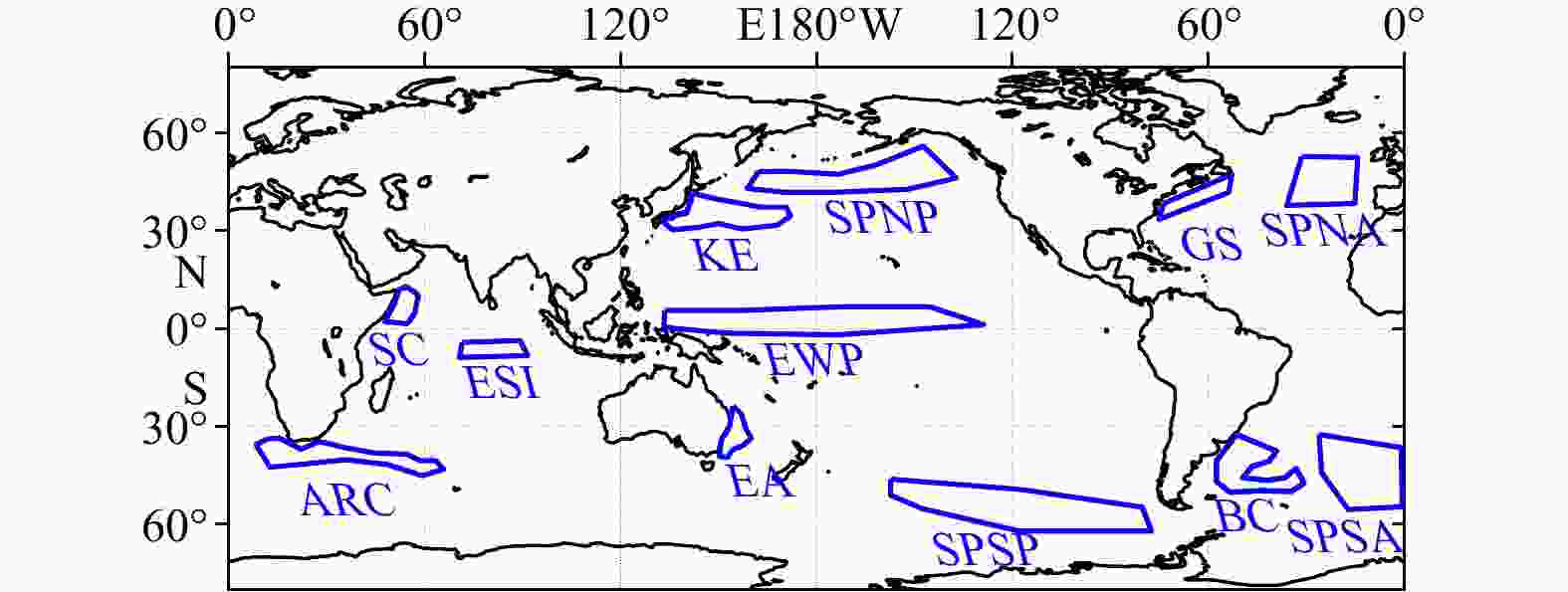
Figure 7. Regions used in Table 2.
Table 1. Formulae of the mean energy terms and conversion rate using the REM, PREM, and RUM methods
Energy term REM PREM RUM $ \dfrac{2}{{\rho }_{0}}\mathrm{T}\mathrm{K}\mathrm{E} $ $ \left[{u}^{2}\right]+\left[{v}^{2}\right] $ $ \langle{u}^{2}\rangle+\left\langle{{v}^{2}}\right\rangle $ $ \langle{u}^{2}\rangle+\left\langle{{v}^{2}}\right\rangle $ $ \dfrac{2}{{\rho }_{0}}\mathrm{M}\mathrm{K}\mathrm{E} $ $ {\left[u\right]}^{2}+{\left[v\right]}^{2} $ $ {\langle u\rangle}^{2}+{\left\langle{v}\right\rangle}^{2} $ $ \langle{\langle u\rangle}^{2}\rangle+\langle{\langle v\rangle}^{2}\rangle $ $ \dfrac{2}{{\rho }_{0}}\mathrm{E}\mathrm{K}\mathrm{E} $ $ \left[{u}^{2}\right]-{\left[u\right]}^{2}+\left[{v}^{2}\right]-{\left[v\right]}^{2} $ $ \langle{u}^{2}\rangle-{\langle u\rangle}^{2}+\langle{v}^{2}\rangle-{\langle v\rangle}^{2} $ $ \langle{u}^{2}\rangle+\langle{\langle u\rangle}^{2}\rangle-2\langle u\langle u\rangle\rangle+ $$ \langle{v}^{2}\rangle+\langle{\langle v\rangle}^{2}\rangle-2\langle v\langle v\rangle\rangle $ $ \dfrac{1}{{\rho }_{0}}\mathrm{R}\mathrm{K}\mathrm{E} $ 0 0 $ \langle u\langle u\rangle\rangle-\langle{\langle u\rangle}^{2}\rangle+ $$ \langle v\langle v\rangle\rangle-\langle{\langle v\rangle}^{2}\rangle $ $ \dfrac{1}{{\rho }_{0}}\mathrm{B}\mathrm{T}\mathrm{R} $ $ \left(\left[{u}^{2}\right]-{\left[u\right]}^{2}\right)\dfrac{\partial \left[u\right]}{\partial x}\;+ $
$ \left(\left[uv\right]-\left[u\right]\left[v\right]\right)\left(\dfrac{\partial \left[u\right]}{\partial y}+\dfrac{\partial \left[v\right]}{\partial x}\right)+ $
$ \left(\left[{v}^{2}\right]-{\left[v\right]}^{2}\right)\dfrac{\partial \left[v\right]}{\partial y} $$ \left(\left\langle{{u}^{2}}\right\rangle-{\left\langle{u}\right\rangle}^{2}\right)\dfrac{\partial \left\langle{u}\right\rangle}{\partial x}\;+ $
$ \left(\left\langle{uv}\right\rangle-\left\langle{u}\right\rangle\left\langle{v}\right\rangle\right)\left(\dfrac{\partial \left\langle{u}\right\rangle}{\partial y}+\dfrac{\partial \left\langle{v}\right\rangle}{\partial x}\right)+ $
$ \left(\left\langle{{v}^{2}}\right\rangle-{\left\langle{v}\right\rangle}^{2}\right)\dfrac{\partial \left\langle{v}\right\rangle}{\partial y} $$ \left\langle{\left\langle{{\left(u-\left\langle{u}\right\rangle\right)}^{2}}\right\rangle\dfrac{\partial \left\langle{u}\right\rangle}{\partial x}}\right\rangle+ $
$ \left\langle{\left\langle{\left(u-\left\langle{u}\right\rangle\right)\left(v-\left\langle{v}\right\rangle\right)}\right\rangle\dfrac{\partial \left\langle{u}\right\rangle}{\partial y}}\right\rangle+ $
$ \left\langle{\left\langle{\left(u-\left\langle{u}\right\rangle\right)\left(v-\left\langle{v}\right\rangle\right)}\right\rangle\dfrac{\partial \left\langle{v}\right\rangle}{\partial x}}\right\rangle+ $
$ \left\langle{\left\langle{{\left(v-\left\langle{v}\right\rangle\right)}^{2}}\right\rangle\dfrac{\partial \left\langle{v}\right\rangle}{\partial y}}\right\rangle $Note: The terms in the first column are averaged over the entire record in REM and are therefore time-independent (i.e., the [·] operator is applied); and running-averaged over a moving window of a pre-defined length in PREM and RUM (i.e., the $\langle {\cdot} \rangle $ operator is applied). Table 2. Comparison between EKE estimated by the PREM and RUM methods in various regions shown in Fig. 7
Region MEAN STD RMSD MIN
CORRABS REL ABS REL ABS REL SPNP 1.38 0.44 1.63 1.81 2.47 2.08 0.38 KE 33.13 0.33 36.7 1.08 60.30 1.54 0.66 EWP 7.26 0.25 13.36 1.59 17.57 1.90 0.52 ESI 3.92 0.17 5.80 0.90 8.01 1.18 0.73 GS 17.69 0.16 17.35 0.49 33.52 0.87 0.69 SPNA 2.53 0.30 2.88 0.67 4.70 1.09 0.55 SPSA 1.51 0.33 2.17 1.08 3.23 1.55 0.62 ARC 16.93 0.15 16.59 0.55 29.82 0.90 0.73 BC 7.38 0.12 6.36 0.42 16.94 1.19 0.47 EA 6.46 0.05 7.49 0.19 15.74 0.49 0.85 SC 5.49 0.06 4.79 0.26 16.34 0.54 0.84 SPSP 3.56 0.26 3.58 0.61 6.42 0.88 0.73 Note: The compared quantities include: difference of time-mean EKE (MEAN), difference of interannual standard deviation (STD), and root-mean-square difference (RMSD), each of these are presented in terms of the absolute difference (ABS) in J/m3, and the relative difference (REL). MEAN REL is relative to the mean EKE of RUM. STD REL and RMSD REL are relative to the standard deviation of RUM. The numbers are the maximum values in each region. The last column shows the minimal correlation coefficient (MIN CORR) between PREM and RUM EKEs. SPNP: subpolar North Pacific; KE: Kuroshio Extension; EWP: equatorial West Pacific; ESI: equatorial South Indian; GS: Gulf Stream; SPNA: subpolar North Atlantic; SPSA: subpolar South Atlantic; ARC: Agulhas Return Current; BC: Brazil Current; EA: East Australia; SC: Somali Current; SPSP: subpolar South Pacific. -
Akuetevi C Q C, Barnier B, Verron J, et al. 2016. Interactions between the Somali Current eddies during the summer monsoon: Insights from a numerical study. Ocean Science, 12(1): 185–205, doi: 10.5194/os-12-185-2016 Beal L M, Donohue K A. 2013. The Great Whirl: Observations of its seasonal development and interannual variability. Journal of Geophysical Research: Oceans, 118(1): 1–13, doi: 10.1029/2012JC008198 Bonaduce A, Cipollone A, Johannessen J A, et al. 2021. Ocean mesoscale variability: a case study on the mediterranean sea from a re-analysis perspective. Frontiers in Earth Science, 9: 724879, doi: 10.3389/feart.2021.724879 Bower A S, Armi L, Ambar I. 1995. Direct evidence of meddy formation off the southwestern coast of Portugal. Deep-Sea Research Part Ⅰ: Oceanographic Research Papers, 42(9): 1621–1630, doi: 10.1016/0967-0637(95)00045-8 Bower A S, Armi L, Ambar I. 1997. Lagrangian observations of meddy formation during a mediterranean undercurrent seeding experiment. Journal of Physical Oceanography, 27(12): 2545–2575, doi: 10.1175/1520-0485(1997)027<2545:LOOMFD>2.0.CO;2 Chen Ru, Flierl G R, Wunsch C. 2014. A description of local and nonlocal eddy–mean flow interaction in a global eddy-permitting state estimate. Journal of Physical Oceanography, 44(9): 2336–2352, doi: 10.1175/JPO-D-14-0009.1 Chen Xiao, Qiu Bu, Chen Shuiming, et al. 2015. Seasonal eddy kinetic energy modulations along the North Equatorial Countercurrent in the western Pacific. Journal of Geophysical Research: Oceans, 120(9): 6351–6362, doi: 10.1002/2015JC011054 Chen Ru, Thompson A F, Flierl G R. 2016. Time-dependent eddy-mean energy diagrams and their application to the ocean. Journal of Physical Oceanography, 46: 2827–2850, doi: 10.1175/JPO-D-16-0012.1 Cheng Yu-Hsin, Ho Chung-Ru, Zheng Quanan, et al. 2014. Statistical characteristics of mesoscale eddies in the North Pacific derived from satellite altimetry. Remote Sensing, 6(6): 5164–5183, doi: 10.3390/rs6065164 Cheng Xuhua, McCreary J P, Qiu Bo, et al. 2018. Dynamics of eddy generation in the central Bay of Bengal. Journal of Geophysical Research: Oceans, 123(9): 6861–6875, doi: 10.1029/2018JC014100 Clarke A J. 1983. The reflection of equatorial waves from oceanic boundaries. Journal of Physical Oceanography, 13(7): 1193–1207, doi: 10.1175/1520-0485(1983)013<1193:TROEWF>2.0.CO;2 Di Lorenzo E, Foreman M G G, Crawford W R. 2005. Modelling the generation of Haida Eddies. Deep-Sea Research Part II: Topical Studies in Oceanography, 52(7–8): 853–873, doi: 10.1016/j.dsr2.2005.02.007 Drillet Y, Bourdallé-Badie R, Siefridt L, et al. 2005. Meddies in the Mercator North Atlantic and Mediterranean Sea eddy-resolving model. Journal of Geophysical Research: Oceans, 110(C3): C03016, doi: 10.1029/2003JC002170 Ducet N, Le Traon P Y, Reverdin G. 2000. Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and -2. Journal of Geophysical Research: Oceans, 105(C8): 19477–19498, doi: 10.1029/2000JC900063 Faghmous J H, Frenger I, Yao Yuanshun, et al. 2015. A daily global mesoscale ocean eddy dataset from satellite altimetry. Scientific Data, 2: 150028, doi: 10.1038/sdata.2015.28 Fu L L, Qiu Bo. 2002. Low-frequency variability of the North Pacific Ocean: the roles of boundary- and wind-driven baroclinic Rossby waves. Journal of Geophysical Research: Oceans, 107(C12): 13-1–13-10, doi: 10.1029/2001JC001131 Jia Fan, Wu Lixin, Qiu Bo. 2011. Seasonal modulation of eddy kinetic energy and its formation mechanism in the southeast Indian Ocean. Journal of Physical Oceanography, 41(4): 657–665, doi: 10.1175/2010JPO4436.1 Jouanno J, Sheinbaum J, Barnier B, et al. 2012. Seasonal and interannual modulation of the eddy kinetic energy in the Caribbean Sea. Journal of Physical Oceanography, 42(11): 2041–2055, doi: 10.1175/JPO-D-12-048.1 Kang Dujuan, Curchitser E N. 2015. Energetics of eddy–mean flow interactions in the Gulf Stream region. Journal of Physical Oceanography, 45(4): 1103–1120, doi: 10.1175/JPO-D-14-0200.1 Kang Dujuan, Curchitser E N. 2017. On the evaluation of seasonal variability of the ocean kinetic energy. Journal of Physical Oceanography, 47(7): 1675–1683, doi: 10.1175/JPO-D-17-0063.1 Liang X S. 2012. Multiscale window interaction and localized nonlinear hydrodynamic stability analysis. In: Oh H W, ed. Advanced Fluid Dynamics. IntechOpen, 159–182, https://www.intechopen.com/books/1013 [2012–03–09/2024–01–29] Liang X S. 2016. Canonical transfer and multiscale energetics for primitive and quasigeostrophic atmospheres. Journal of the Atmospheric Sciences, 73(11): 4439–4468, doi: 10.1175/JAS-D-16-0131.1 Liu W T, Xie Xiaosu, Niiler P P. 2007. Ocean–atmosphere interaction over agulhas extension meanders. Journal of Climate, 20(23): 5784–5797, doi: 10.1175/2007JCLI1732.1 Paillet J, Le Cann B, Carton X, et al. 2002. Dynamics and evolution of a northern meddy. Journal of Physical Oceanography, 32(1): 55–79, doi: 10.1175/1520-0485(2002)032<0055:DAEOAN>2.0.CO;2 Penduff T, Barnier B, Dewar W K, et al. 2004. Dynamical response of the oceanic eddy field to the North Atlantic Oscillation: a model–data comparison. Journal of Physical Oceanography, 34(12): 2615–2629, doi: 10.1175/JPO2618.1 Pope S B. 2000. Turbulent Flows. New York, NY, USA: Cambridge University Press Qiu Bo, Chen Shuiming. 2010. Eddy-mean flow interaction in the decadally modulating Kuroshio Extension system. Deep-Sea Research Part Ⅱ: Topical Studies in Oceanography, 57(13/14): 1098–1110, doi: 10.1016/j.dsr2.2008.11.036 Qiu Bo, Chen Shuiming, Schneider N, et al. 2014. A coupled decadal prediction of the dynamic state of the Kuroshio Extension system. Journal of Climate, 27(4): 1751–1764, doi: 10.1175/JCLI-D-13-00318.1 Reynolds O. 1895. On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Gineering sciences, 186: 123–164, doi: 10.1098/rsta.1895.0004 Rogachev K A, Shlyk N V. 2018. The role of the aleutian eddies in the Kamchatka Current warming. Russian Meteorology and Hydrology, 43(1): 43–48, doi: 10.3103/S1068373918010065 Rogachev K A, Shlyk N V. 2019. Characteristics of the Kamchatka Current eddies. Russian Meteorology and Hydrology, 44(6): 416–423, doi: 10.3103/S1068373919060062 Rogachev K, Shlyk N, Carmack E. 2007. The shedding of mesoscale anticyclonic eddies from the Alaskan Stream and westward transport of warm water. Deep-Sea Research Part Ⅱ: Topical Studies in Oceanography, 54(23–26): 2643–2656, doi: 10.1016/j.dsr2.2007.08.017 Saito R, Yamaguchi A, Yasuda I, et al. 2014. Influences of mesoscale anticyclonic eddies on the zooplankton community south of the western Aleutian Islands during the summer of 2010. Journal of Plankton Research, 36(1): 117–128, doi: 10.1093/plankt/fbt087 Seo H. 2017. Distinct influence of air-sea interactions mediated by mesoscale sea surface temperature and surface current in the Arabian Sea. Journal of Climate, 30(20): 8061–8080, doi: 10.1175/JCLI-D-16-0834.1 Serra N, Ambar I. 2002. Eddy generation in the Mediterranean undercurrent. Deep-Sea Research Part Ⅱ: Topical Studies in Oceanography, 49(19): 4225–4243, doi: 10.1016/S0967-0645(02)00152-2 Serra N, Ambar I, Käse R H. 2005. Observations and numerical modelling of the Mediterranean outflow splitting and eddy generation. Deep-Sea Research Part Ⅱ: Topical Studies in Oceanography, 52(3/4): 383–408, doi: 10.1016/j.dsr2.2004.05.025 Trott C B, Subrahmanyam B, Murty V S N. 2017. Variability of the Somali Current and eddies during the southwest monsoon regimes. Dynamics of Atmospheres and Oceans, 79: 43–55, doi: 10.1016/j.dynatmoce.2017.07.002 von Storch J S, Eden C, Fast I, et al. 2012. An estimate of the Lorenz energy cycle for the World Ocean based on the 1/10° STORM/NCEP simulation. Journal of Physical Oceanography, 42(12): 2185–2205, doi: 10.1175/JPO-D-12-079.1 Wang Lei, Yu Jinyi. 2018. A recent shift in the monsoon centers associated with the tropospheric biennial oscillation. Journal of Climate, 31(1): 325–340, doi: 10.1175/JCLI-D-17-0349.1 Wang Sen, Zhu Weijun, Ma Jing, et al. 2019. Variability of the Great Whirl and its impacts on atmospheric processes. Remote Sensing, 11(3): 322, doi: 10.3390/rs11030322 Yang Yang, Liang X S. 2016. The instabilities and multiscale energetics underlying the mean–interannual–eddy interactions in the Kuroshio Extension region. Journal of Physical Oceanography, 46(5): 1477–1494, doi: 10.1175/JPO-D-15-0226.1 Yang Yang, Liang X S. 2019. Spatiotemporal variability of the global ocean internal processes inferred from satellite observations. Journal of Physical Oceanography, 49(8): 2147–2164, doi: 10.1175/JPO-D-18-0273.1 Zenk W, Schultz Tokos K, Boebel O. 1992. New observations of meddy movement south of the Tejo Plateau. Geophysical Research Letters, 19(24): 2389–2392, doi: 10.1029/92GL02139 Zhou Guidi, Cheng Xuhua. 2021. On the errors of estimating oceanic eddy kinetic energy. Journal of Geophysical Research: Oceans, 126(2): e2020JC016449, doi: 10.1029/2020JC016449 Zhou Guidi, Cheng Xuhua. 2022. Impacts of oceanic fronts and eddies in the Kuroshio-Oyashio Extension region on the atmospheric general circulation and storm track. Advances in Atmospheric Sciences, 39(1): 22–54, doi: 10.1007/s00376-021-0408-4 Zhou Guidi, Li Zhuhua, Cheng Xuhua. 2021a. Intrinsic and wind-driven decadal variability of the Kuroshio Extension in altimeter observations. Frontiers in Marine Science, 8: 766226, doi: 10.3389/fmars.2021.766226 Zhou Jiang, Zhou Guidi, Liu Hailong, et al. 2021b. Mesoscale eddy-induced ocean dynamic and thermodynamic anomalies in the North Pacific. Frontiers in Marine Science, 8: 756918, doi: 10.3389/fmars.2021.756918 -





 下载:
下载: